Markus Pilzecker
Ponderomotorische Kräfte
auf bewegte Media
Diplomarbeit
Darmstadt, 2003-03-23
5
Theoretische Quanten-Elektronik
Prof. Dr. Peter Mulser
Institut für Angewandte Physik
Technische Universität Darmstadt
Hochschulstr. 4a
D-64289 Darmstadt

[Bou65]
Dieser Text wurde gesetzt mit LATEX2 <1999/12/01> auf TEX 3.14159 (Web2C version 7.3.1) in einer
kerning-optimierten Variante des Fonts Computer Modern in der Basisgröße 10 Punkt. Die deutschen
Sprachspezifica wurden durch das “german.sty”-Paket 2.5e und die Postscript-Graphiken mit dem “epsfig.sty”-Paket
eingebunden. Als Entwicklungsumgebung diente Xemacs 19.16 mit AucTeX 9.7, wobei Xdvik 20.57 zur
Vorbetrachtung diente. Das gesamte TEX-Paket war eine leicht modifizierte Variante der teTEX-Distributionis für
Linux in der Versioni 1.0.7. Die Rechnerplattform war ein unter Redhat-Linux 5.0, Kernel 2.2.14 laufender
Am486.
<1999/12/01> auf TEX 3.14159 (Web2C version 7.3.1) in einer
kerning-optimierten Variante des Fonts Computer Modern in der Basisgröße 10 Punkt. Die deutschen
Sprachspezifica wurden durch das “german.sty”-Paket 2.5e und die Postscript-Graphiken mit dem “epsfig.sty”-Paket
eingebunden. Als Entwicklungsumgebung diente Xemacs 19.16 mit AucTeX 9.7, wobei Xdvik 20.57 zur
Vorbetrachtung diente. Das gesamte TEX-Paket war eine leicht modifizierte Variante der teTEX-Distributionis für
Linux in der Versioni 1.0.7. Die Rechnerplattform war ein unter Redhat-Linux 5.0, Kernel 2.2.14 laufender
Am486.
Die Liniengraphiken wurden mit Xfig 3.1.3 erstellt und im Postscript-Format zur Verfügung gestellt. Der Index wurde
mit R.L. Aurbachs IdxTeX 2.1 erzeugt. Die Bibliographie wurde mit Oren Patashniks BibTEX 0.99c mit einem
modifizierten “alpha”-Stil erzeugt. Zum Teil wurde die Literatur am Fachinformationszentro Karlsruhe in der
Datenbank INSPEC recherchiert, mit Markus Pilzeckers “inspec2bibtex.awk” ins BibTEX-Format konvertiert und
mit Gerd Neugebauers BibTool 2.39 nachbereitet.
Die Druckaufbereitung erfolgte mit dvipsk 5.86, Angus Duggans psutils-p17 psbook, psnup
und psselect, und Peter L. Deutschs Aladdin Ghostscript 5.10 mit einer Floyd-Steinberg-
dithernden Umsetzung auf PCL 5. Der Druck selbst erfolgte auf einem HP-Laserjet
8000N1 auf Arches
Expression Briefpapier natur2
.
Die Buchdruckerei Günther Walch, Saarbrücken, unterstützte Auswahl, Beschaffung und Schnitt des Papiers, die
Buchbinderei Kittler und Jäger, Saarbrücken, besorgte das Binden.
Alle Verwertungsrechte für diese Arbeit liegen
beim Autori.
Jede über das
Lesen eines der vom Autori selbst verlegten
Exemplare hinausgehende Verwertung bedarf
dessen schriftlicher Erlaubnis.
Inhalt
Zusicherung
Diese Arbeit ist das geistige Produkt des Autoris und ausschließlich mit zulässigen Mitteln
erstellt.
Ehrerbietungen
Trotzdem hat natürlich vieles zum Entstehen dieser Arbeit beigetragen. Insbesondere haben einige
meiner Mitmenschen mehr oder weniger direkt diese Arbeit gefördert und befruchtet, wofür hier
gedankt sei:
- meinen Eltern für die Grundsteine zu meiner Persönlichkeit und für die materielle
Unterstützung
- meinem Freundeskreis allgemein für den Antrieb und die Kritik und insbesondere Stefan
Trcek für viele fruchtbare Diskussiones und das Korrekturlesen
- den vielen von der Idee der freien Software beseelten Softwerkern, ohne deren Einsatz
und deren Produkte diese Arbeit in vielerlei Hinsicht erheblich mühevoller gewesen wäre
- allen Streitern für ein freies Netz
- den Vordenkern
- Noam Chomsky für sein Zusammenführen von Linguistik und Mathematik und für
das Vorbild als politischer Intellektueller
- Niklaus Wirth und Bertrand Meyer für ihren Protagonismum beim Entwurf von
Formalsprachen
- Donald Knuth für seine Inspirationem zum Fontdesign und Textsatz
- Kurt Tucholsky und Ernst Jandl für die Einsicht, daß Sprache mehr ist
- Albert Einstein, Hermann Weyl, Johann von Neumann, P.A.M. Dirac und den
in der Bibliographie genannten Autoribus, insbesondere Hermann Ludwig von
Helmholtz, Lew Davidowitsch Landau und Sybren Ruurds de Groot für ihren
Pragmatismum und die Grazie in der Physik
- Prof. Dr. Peter Mulser für seinen gesamtheitlicheren Blick auf die Physik, für die durch seine
sorgfältig vorbereiteten Vorlesungen geweckte Neugier auf dieses Forschungsgebiet, für viele
Diskussiones am Detail und nicht zuletzt seine Geduld
.
Kapitel 1
Prolog
1.1 Was sind ponderomotorische Kräfte ?
Bringt man [geladene Teilchen enthaltende] Materie mit elektromagnetischer Strahlung [,
z.B. Licht] zur Wechselwirkung, dann beobachtet man makroskopisch und säkular das folgende
Phänomen:
Licht und Materie tauschen Impuls aus1.
Die Kraft, die die Materie auf die elektromagnetische Strahlung ausübt, ist proportional dem
Intensitäts-Gradienten der Strahlung und zeigt auch in dessen Richtung [Kib66]. Die Reactio auf die
Materie zeigt natürlich genau in die entgegengesetzte Richtung.
Im Frequenzbereich sichtbaren Lichtes werden ponderomotorische Kräfte etwa ab
Intensitäten von 1012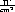 relevant. Diese Intensitäten werden von modernen Hochleistungs-
Lasern um mittlerweile bis zu acht Zehner-Potenzen überschritten. Das Handhaben
von Intensitäten um 1019
relevant. Diese Intensitäten werden von modernen Hochleistungs-
Lasern um mittlerweile bis zu acht Zehner-Potenzen überschritten. Das Handhaben
von Intensitäten um 1019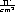 gehört für viele Forschergruppen schon zum Alltag.
Insbesondere die Erkenntnis, daß ponderomotorische Kräfte schon bei Wellenzügen von
wenigen2
Wellenlängen auftreten, ermöglichte es, Experimente erfolgreich mit Lasern durchzuführen, deren
Leistungsdichte durch Verkürzen der Pulsdauer erhöht wurde.
gehört für viele Forschergruppen schon zum Alltag.
Insbesondere die Erkenntnis, daß ponderomotorische Kräfte schon bei Wellenzügen von
wenigen2
Wellenlängen auftreten, ermöglichte es, Experimente erfolgreich mit Lasern durchzuführen, deren
Leistungsdichte durch Verkürzen der Pulsdauer erhöht wurde.
1.2 Anwendungen
1.2.1 Inertial-Kernfusion
Eine große Triebkraft, die Erforschung ponderomotorischer Kräfte voranzutreiben, ist die Inertial-
Kernfusion, von der man erwartet, daß sie ergiebiger und sauberer einen Beitrag zur
Energieversorgung liefern kann als die umstrittene Kernspaltung.
Hier zielt man darauf ab, ein kleines wasserstoffhaltiges Target durch allseitiges
Beleuchten mit hoher Intensität soweit komprimieren und gleichzeitig
aufheizen3
zu können, daß eine Kernfusion zündet.
1.2.1.1 Instabilitäten
Die ernüchternden Ergebnisse der ersten na¨iven Experimente, das Target konzentrisch mit mehreren
Laser-Teil-Strahlen zu beschießen, zeigten schnell, daß die Natur vor die erfolgreiche Inertial-
Kernfusion das tiefe Verstehen einer ganzen bunten Palette von Instabilitäts-Phänomenen gestellt
hat.
Zu den Instabilitäten, bei deren Zustandekommen ponderomotorische Kräfte eine wesentliche Rolle
spielen, gehören die
-
Filamentation,
- bei der transversale Intensitätsschwankungen sich immer mehr aufsteilen
-
die stimulierte Raman-Streuung,
- bei der die einfallende Lichtwelle in eine Elektron-
Plasma-Welle und eine gestreute Lichtwelle zerlegt wird
-
die stimulierte Brillouin-Streuung,
- bei der die einfallende Lichtwelle in eine
ionenakustische Welle und eine gestreute Lichtwelle zerlegt wird
.
Von diesen dreien sei im Rahmen dieses einleitenden Appetit-Happens folgend nur die wohl am
leichtesten verständliche Filamentation näher dargestellt:
Filamentation
Die Tatsache, daß ein Laserstrahl über seinen Querschnitt Intensitätsschwankungen aufweist -
meist sogar mit mehreren lokalen Maximis und Minimis - führt beim Durchgang eines solchen
Strahles sehr hoher Intensität durch Materie zum Aufbrechen dieses Strahles in mehrere Filamente.
Das rührt daher, daß der Intensitäts-Gradient rund um ein lokales Maximum aus allen Richtungen
radial auf dieses Maximum zeigt, d.h. die Materie drückt aus allen Richtungen radial auf das in
diesem Maximo gefangene Licht und schnürt es weiter ein. Das Maximum wird noch
größer, der Gradient noch steiler und so fort ... . Im Gegenzug wird natürlich die Materie
aus dem entstandenen hoch-intensiven Filament verdrängt. Aus dem Gesagten ist klar,
daß Filamentation eine der großen Alltags-Herausforderungen an jeden Hochleistungs-
Laser-(Betreiber bzw. Bauer) darstellt, denn jede noch so kleine radiale Schwankung der
Intensität4
steilt sich von einer optischen Komponente zur nächsten immer weiter auf und führt, wenn sie nicht
schon in ausreichend frühem Stadio den Laser verlassen und das [“rettende”] Target erreicht hat,
zu erheblichen Schäden an der Apparatur.
1.2.1.2 Stand der Technik
Als möglicher Ausweg, der verspricht, viele der angedeuteten Probleme gleichzeitig beherrschbar zu
machen, erscheint zur Zeit, ein kugelförmiges Target in einen konzentrischen “Ofen” zu plazieren
und es dort mit sekundärer Röntgen-Hohlraum-Strahlung gleichzeitig aufzuheizen und zu
komprimieren. “Sekundär” heißt hier, daß man die innere Ofen-Oberfläche mit Laserlicht bestrahlt,
wobei sich diese soweit aufheizt, daß sie thermische Röntgen-Strahlung emittiert, die den Hohlraum
des Ofens dann sehr homogen und isotrop erfüllt. Dabei werden sowohl die Absorption wesentlich
verbessert5
als auch die Schwankungen der Beleuchtungs-Intensität auf ein Maß reduziert, das mit
direkter Laser-Bestrahlung des Targets kaum zu erreichen wäre und Voraussetzung dafür
ist, daß man nicht an Rayleigh-Taylor-Instabilitäten und Filamentations-Phänomenen
scheitert.
Nach einleitend Gesagtem wäre man nun vielleicht versucht, zu vermuten,
daß der longitudinale Intensitätsgradient des Lichtes vom Target weg, dieses
komprimiert6.
Es hat sich aber erwiesen, daß nicht ponderomotorische Kräfte selbst den entscheidenden Anteil
liefern, der das Target komprimiert, sondern vielmehr der Ablationsdruck.
1.3 Ein Blick ins Mikroskopische
Bevor wir uns in der eigentlichen Arbeit darauf stürzen, ponderomotorische Kräfte genauer zu
berechnen, möchte ich noch an einem einfachen Beispiel im Detail aufzeigen, wie ponderomotorische
Kräfte zustande kommen.
Dazu betrachten wir ein geladenes Teilchen, das sich gerade in einer sich von links nach rechts
[in y-Richtung] ausbreitenden, linear polarisierten elektromagnetischen Welle befindet.
Die Intensität dieser Welle nehme in Ausbreitungsrichtung linear ab, d.h. mit der Zeit linear zu.
Der elektrische Anteil des Feldes zeige in x-Richtung, der magnetische Anteil des Feldes in
z-Richtung. Die Anfangsbedingungen sind so gewählt [, d.h. das Koordinatensystem ist so gelegt],
daß das Oszillationszentrum der Bahn des Teilchen sich zum Beobachtungszeitpunkt t = 0 am Ort
(0,y0,0) in Ruhe befand.
Da das Teilchen unter diesen Umständen eine ebene Bahn in z = 0 beschreibt, wurde in
Abbildung 1.2 die redundante z-Koordinate zugunsten der Darstellung des zeitlichen Verlaufs
(t-Koordinate) unterdrückt, d.h. der magnetische Anteil des Feldes liegt parallel zur
t-Achse.
Man sieht, daß die Teilchenbahn aus einer einer säkularen [raumzeitlichen] Parabel überlagerten
hochfrequenten liegenden Acht besteht. In anderen Fällen, wie der longitudinalen Plasmawelle oder
der linear polarisierten stehenden Welle, nimmt der hochfrequente Anteil der Trajektorie eine
andere Form an ( gerade Strecke bzw. Sichel
gerade Strecke bzw. Sichel ) - ohne daß sich am Phänomen der säkularen
Beschleunigung etwas ändern würde. In jedem Falle “sammelt” das Teilchen in den Passagen der
Bahn, die durch Gebiet schwächeren Feldes laufen, weniger Impuls in der einen Richtung, als es im
Gebiet stärkeren Feldes [also Gradient aufwärts] in der anderen Richtung erfährt. Bei jedem
Durchlauf akkumuliert sich so immer mehr Impuls, der das Oszillationszentrum des Teilchens in
seine Richtung zieht.
) - ohne daß sich am Phänomen der säkularen
Beschleunigung etwas ändern würde. In jedem Falle “sammelt” das Teilchen in den Passagen der
Bahn, die durch Gebiet schwächeren Feldes laufen, weniger Impuls in der einen Richtung, als es im
Gebiet stärkeren Feldes [also Gradient aufwärts] in der anderen Richtung erfährt. Bei jedem
Durchlauf akkumuliert sich so immer mehr Impuls, der das Oszillationszentrum des Teilchens in
seine Richtung zieht.
Kapitel 2
Metalog
2.1 Erkenntnistheoretisches
Wir kennen alle die beiden großen Epochen wissenschaftlichen Tuns:
- die griechische Klassik der argumentativen Wissenschaft “im Elfenbeinturm”,
- die “moderne”, post-galile¨ische Art zu wissenschafteln, bei der der Folgerungsraum
postulierter Theorien sich mit seiner der Realität zugewandten Oberfläche beständig an
dieser messen lassen muß
. Die Siege der großen Revolutionum der Naturwissenschaft waren immer Siege des Pragmatismi:
- Galileo Galile¨i hat der Theorie die Prüfung an der Realität verordnet,
- Einstein hat die Zeitmessung am Machbaren orientiert,
- die Quantenmechaniker hatten ein Einsehen in die Grenzen des Meßprozesses, wenn die
Systeme klein werden
. Auch wenn diese Realitäts-Zugewandtheit die großen Fortschritte geebnet hat, hat doch der
aristotelische Standpunkt nie gänzlich an Bedeutung verloren. Er wirkt nur heute in zweierlei
Hinsicht im Hintergrund weiter:
- als Baustein-Kasten á la Lego hilft er dem Wissenschaftler, neue Theorien zu gebären,
- als stetig ordnendes Moment, das kraft tiefergehenden Einsehens danach trachtet, die
vorhandenen Theorien zu verschlanken1,
ist er der große Ökonom in der Wirtschaft der Wissenschaft
.
Hiesige Arbeit trägt wesentlich die Züge des ordnenden Momenti: sie erklärt einige Bezüge zwischen
Inseln bisheriger Erkenntnis und sie zelebriert die Tauglichkeit eines Teils unseres Werkzeugkastens
zu diesem Behufe.
2.2 Ergonomisches
2.2.1 Kommunikation
Ein durchaus nennenswerter Teil wissenschaftlicher Arbeit besteht darin, bereits in verschiedenen
Veröffentlichungen publizierte Kenntnis zusammenzutragen, zu verstehen und zu filtern. Die
Prozesse des Verstehens und des Filterns machen es notwendig, sich mit verschiedenen Sicht- und
oft uneinheitlichen Darstellungsweisen auseinanderzusetzen. Hat dies auch oft ein kreatives Moment,
so wiegt dennoch, gerade bei Stoff, der schon weitgehend seine Reife gefunden hat, die Last des
Unhandlichen manchmal schwer.
2.2.1.1 Redundanz
Auch diese Arbeit enthält deshalb vieles, das in der einen oder anderen Form bereits an
anderer Stelle veröffentlicht wurde. Dem Leser die Last des Zusammentragens und des
Unergonomischen der verschiedenen Darstellungen zu nehmen, rechtfertigt hoffentlich die
unvermeidlich damit einhergehende noch weiter wachsende Redundanz in der Flut veröffentlichten
Papiers.
2.2.1.2 Controlled Language
Aus der Erkenntnis, daß sprachliche Polymorphie technische Kommunikation eher erschwert,
erwuchs das Ansinnen, die Sprache dieser Arbeit einer technischen, in ferner Zukunft vielleicht sogar
automatisch parsbaren, einige zaghafte Schritte näher zu bringen. Voraussetzung, damit eine
Sprache die gehörige Akzeptanz der Community einer Domäne findet, ist ihre Performanz, d.h. ihre
Fähigkeit, möglichst alles Denkbare dieser Domäne artikulieren zu können. Die im nächsten
Abschnitt diskutierte Tensorschreibweise als eine der explizitesten verfügbaren Schreibweisen für
Elementa linearer Räume mag hierfür ein Beispiel sein. Zwei weitere Symptome, die hier zu finden
sein werden, sind die den Chomsky-Typ3-Sprachen entlehnten, zu Beginn von Unterkapitel 2.3
genannten Elementa, die einige Meta-Konstruktiones der deutschen Sprache explizit
machen, sowie die der Unterkapitel-Hierarchie untergeordneten Deklarationes verwendeter
Formelzeichen2.
Tensorschreibweise
Statt der eher aus der Mathematik gewohnten indexlosen Vektorschreibweise wird hier ausschließlich
die sonst [z.B.] in der Differentialgeometrie und Relativitätstheorie übliche [Koordinaten-]Index-
Schreibweise zelebriert. Damit wird das schlanke Erscheinungsbild ersteren Notierstils der
präziseren, aber leider unübersichtlicheren Darstellung geopfert. Allerdings lehrt die Erfahrung,
daß Übersichtlichkeit ein stark der Seh-Erfahrung auf jeweiligem Terrain assozi¨iertes Phänomen
darstellt3.
Ich hoffe, das relativiert den Tribut an die Genauigkeit. Der Preis, den die Community in Form
z.B. jahrzehnte-währender Diskussionis um das richtige Verjüngen im Kelvin’schen Ausdruck für
die ponderomotorische Kraft gezahlt hat, erscheint mir ein ungleich höherer.
2.2.1.3 Konzept-Index
Der Begriffs-Index am Ende der Arbeit versucht, alle wichtigen Nominal-Phrasen, die der Text
anführt, zu katalogisieren. Die [wichtigeren der] einzelnen Worte jeder aufgenommenen
Nominalphrase werden im Index wiederum permutiert, um sie in der Sortierung an die Pole-
Positition zu manövrieren. Dadurch soll dem Text auch der selektive Zugang - quasi mit der Lupe -
eröffnet werden.
2.3 Syntaktisches
2.3.1 Non-Terminal-Symbole
Global bezüglich des gesamten Dokumentes gelten die folgenden syntaktischen
| ( ) | - eingeklammerter Ausdruck wird zuerst ausgewertet, |
| | - Argumentliste einer Funktionis |
| |
| |
| [] | - expandiert zu (0- bis 1-)mal dem eingeklammerten String, |
| | - aber per Konventionem sind auch Literatur-Referenzen so notiert |
| { } | expandiert zu (0- bis n  IN-)mal dem eingeklammerten String IN-)mal dem eingeklammerten String |
| | | Alternative |
(  ) ) | Kommentarklammern |
| |
| |
| |
| |
2.3.2 Reichweite von Vereinbarungen
2.3.2.1 Vererbung
Für eine bestimmte Text-Entität gültige Vereinbarungen werden zu deren Beginn getroffen. Sie
werden an alle Sub-Entitäten ererbt, können dort aber lokal überlagert werden.
2.3.2.2 Gültigkeitsbereich von Variablen
In Bezug auf Variablen bedeutet das, daß diese stets zu Beginn eines Kapitels, Unterkapitels,
... vereinbart werden und lokal zu diesem gelten.
Ein Index, über den der durch ihn indizierte Term summiert wird, ist eine zu diesem Termino lokale
Variable. Ein gleichnamiger Index in einem Bruder-Termino[, d.h. einem Termino, der im
Ableitungsbaum4
[des Ausdrucks] auf gleicher Höhe steht] ist eine völlig autarke Größe.
2.3.2.3 Globale Variablen
Der mit Vorgesagtem angemessene Ort für die Deklarationem zum gesamten Dokument
globaler Variablen hätte übergeordnet zur gesamten Kapitelstruktur ganz zu Beginn
liegen müssen. Den ohne hiesige Kenntnis unbedarften Leser hätten wir dort aber sicher
irritiert.
Deshalb deklarieren wir nun hier global für das gesamte Dokument folgende
 () : () : | Dirac’sche Deltafunktion |
 ijk : ijk : | total-antimetrischer Tensor dritter Stufe |
| t : | Zeit50 |
| R : | Ort |
 : : | Winkelfrequenz |
| c : | Lichtgeschwindigkeit5 |
| h : | Planck’sches Wirkungsquantum |
 0 : 0 : | Konstante der dielektrischen Suszeptibilität des Vakui |
 0 : 0 : | Konstante der magnetischen Suszeptibilität des Vakui |
| e : | Elementarladung50 |
| E : | makroskopisches elektrisches Feld |
| B : | makroskopisches magnetisches Feld |
| D : | makroskopische dielektrische Verschiebung |
| H : | makroskopische magnetische Induktion |
| P : | makroskopische freie Ladungsdichte |
| J : | makroskopische freie Stromdichte |
| P : | makroskopische Polarisation |
| M : | makroskopische Magnetisierung |
| : |
| : |
| : |
| : |
| : |
2.3.3 Deklination von Fremdworten
Substantivisch auftretende Fremdworte sind entsprechend ihrem aktuellen
Kasui dekliniert6.
Dieses Vorgehen ist als Experiment zu verstehen und möge zu eigenen kritischen Gedanken den
Gebrauch von Fremdworten betreffend anregen. Eine vorläufig rückblickende Kritik des
Autoris hierzu findet sich im Epilog.
2.3.4 Formeln
2.3.4.1 (Klein- und Groß-)schreibung
Sofern beide im Verlaufe der Darstellung auftreten, sind “Vakuum”-Größen klein und
hydrodynamische [d.h. ensemble-gemittelte] Größen groß gesetzt. Sonst wurden zugunsten der
Lesbarkeit in der Szene etablierte Schreibweisen beibehalten.
2.3.4.2 Indices und Variablen des Minkowski-Raums
Zeit-räumliche Größen werden als Elementa eines Minkowski-Raumes behandelt, dessen 0-te
Koordinate die zeitliche ist und dessen räumliche Koordinaten mit 1, 2 und 3 numeriert
sind.
Mit griechischen Buchstaben sind Indices über der Grundmenge {0, 1, 2, 3} notiert, d.h. damit
werden alle Minkowski-Koordinaten durchgezählt. Mit lateinischen Buchstaben sind Indices über
der Grundmenge {1, 2, 3} notiert, d.h. daß damit nur die Raumkoordinaten indiziert
sind.
Die Zeit-Koordinate des Minkowski-Raums wird auf Längeneinheiten abgebildet, indem die
Laborzeit t mit der Lichtgeschwindigkeit c multipliziert wird. Demzufolge ersetzt  0 :=
0 :=  die
partielle Ableitung nach der Zeit und analog d0 :=
die
partielle Ableitung nach der Zeit und analog d0 :=  die totale. Wird eine Größe x nach der [so
“vereinheitlichten”] Zeit-Koordinate abgeleitet, dann werden wir meistens die in der
Differentialgeometrie übliche Schreibweise
die totale. Wird eine Größe x nach der [so
“vereinheitlichten”] Zeit-Koordinate abgeleitet, dann werden wir meistens die in der
Differentialgeometrie übliche Schreibweise
verwenden. Sie imitiert am überzeugendsten den sonst allgegenwärtigen Punkt  .
.
2.3.4.3 Metrik
Die Metrik ist
.
2.3.4.4 Tensores
als Ganzes schreiben wir mit einfachen lateinischen Buchstaben.
Tensorkomponenten werden, wie üblich
notiert, wenn die Stufe des Tensoris vorgegeben ist. Eine solche Tensorkomponente ist immer als
Repräsentant für alle konkreten Setzungen der Indicum i,j,...,l zu verstehen.
Komponenten eines Tensoris T, dessen Stufe n Gegenstand einer Parametrierung ist, notieren wir
.
Sind von den Komponenten eines Tensoris T (l + n)-ter Stufe l Stufen konkret vorgegeben und
die weiteren n Stufen nur der Anzahl der Stufen nach spezifiziert, dann notieren wir
.
2.3.4.5 Dyadische Produkte
Existiert im aktuellen Scope bereits ein Vektor r, dann sei unter dem n-stufigen Tensori
zu verstehen.
2.3.4.6 Einsteins Summierkonvention
Tritt in einem Termino ein Index sowohl als oberer als auch als unterer auf, so ist dieser Term
über die Grundmenge dieses Indicis zu summieren auch ohne daß die Summe explizit
notiert wird. So ist das verjüngende Produkt ST zweier Tensorum S und T definiert als
.
Im Falle zweier Tensorum S und T nicht a priori festgelegter Stufe n ( (2.4a)
(2.4a) ), ist über alle
möglichen Permutationes der n Indicum zu summieren:
), ist über alle
möglichen Permutationes der n Indicum zu summieren:
.
2.4 Physikalische Einheiten
implementieren ein Konzept abstrakter Datentypen in der Physik.
Dabei wird jedem Potenzprodukt sogenannter Basis-Einheiten ein eigener Datentyp zugeordnet. Es
existieren für jeden Datentyp Methoden mit den Namen der üblichen mathematischen Operatorum,
die für jede mögliche Kombinationem mit anderen Datentypen den Ergebnistyp festlegen. So kann
bereits mit syntaktischen Mitteln entschieden werden, ob ein gegebener Algorithmus typkonsistent
ist.
Im gesamten Dokument werden die physikalischen Größen in MKSA-Einheiten dargestellt.
Diese Wahl hat folgende Gründe:
- Mit der gegenüber den cgs-Einheiten zusätzlichen Einheit für den elektrischen Strom
wird das Typkonzept rigider.
- Die Typen werden feiner granuliert, was eine strengere Konsistenz-Prüfung von
Algorithmen auf rein syntaktischer Basis ermöglicht.
Kapitel 3
Marktlage
Es soll hier nicht versucht werden, den zahlreichen Übersichten über in der Vergangenheit versuchte
Ansätze zum Thema ponderomotorische Kräfte eine weitere hinzuzufügen, die ihrer Aufgabe im
gegebenen Rahmen nicht gerecht werden könnte. Stattdessen sei auf die verhältnismäßig
ausführliche [und noch einigermaßen aktuelle] Arbeit von Kentwell und Jones [KJ87] verwiesen. Aus
heutiger Sicht bedarf diese jedoch meines Erachtens noch einer Ergänzung um vier Ansätze, die
folgend kurz skizziert seien:
3.1 Kräfte auf Einzelteilchen
3.1.1 Kruskal-Littlejohn-Balescu-Weyssow
In der Kentwellschen Systematik unter die Einzelteilchen- und Lie-Transformations-Formulierungen
(dort Abschnitt 6.2) einzureihen ist ein Verfahren, das Balescu und Weyssow in verschiedenen
Veröffentlichungen [BW86], [BW87], [BW88] dargelegt haben.
3.1.1.1 Historische Wurzeln
Eine Grundlage dieses Verfahrens bildet die Theorie der Lie-Gruppen und
-
Algebren1,2,
die in Ansätzen schon Hermann Weyl Anfang der dreißiger Jahre [Wey31] ins Blickfeld der Physiker
befördert hat. Nachdem Dirac 1949 [Dir49] noch einmal ihre Bedeutung hervorhob, trat sie
schließlich zusehends ihren Siegeszug in physikalische Theorien an. Balescu hat daran in der
Traditioni der Arbeiten von z.B. Currie, Jordan und Sudarshan 1963, [CJS63], Currie [Cur63],
zusammen mit Kotera [BK67] und Piña [BKP67],..., mitgewirkt. Dieses Wirken gipfelt in seinem
1988 veröffentlichten Buch “Transport Processes in Plasmas” [Bal88], in dem er die bzgl. beinahe-
periodischer Teilchentrajektorien wegweisende Arbeit Kruskals [Kru62] mit dem [Anti-]Dogma
Littlejohns [Lit83a], [Lit83b], Transformationes von Phasenraum-Koordinaten nicht auf kanonische
zu beschränken, integrierte.
3.1.1.2 Das Verfahren
In Zusammenarbeit mit Weyssow entstanden hierbei die drei oben zitierten Arbeiten, deren letzte
beiden die Bewegung eines Teilchens in einer sich raumzeitlich nicht allzu schnell ändernden
elektromagnetischen Welle störungstheoretisch beschreiben ( letztere bei zusätzlich
eingeschaltetem “statischen” B-Feld
letztere bei zusätzlich
eingeschaltetem “statischen” B-Feld ).
).
Bei der Separationi von nieder- und hoch-frequentem Bewegungsanteil des in einer in Amplitudine
und Frequenz langsam veränderlichen elektromagnetischen Welle befindlichen geladenen Teilchens
folgt man den Spuren Kruskals und transformiert auf ein Koordinatensystem in dem die Phase des
hochfrequenten Bewegungsanteils als selbständige Koordinate auftritt. Man kann dann zeigen,
daß die die Dynamik beschreibenden Lie-Klammern auf der langsamen Zeitskalanicht
von dieser Phase abhängen und hat sich so des hochfrequenten Anteils der Bewegung
entledigt.
3.1.1.3 Kritik
| m : | Masse des oszillierenden Teilchens |
| q : | Ladung des oszillierenden Teilchens |
 : : | relativistischer metrischer Faktor (1 - (v/c)2)- |
| : |
| : |
| : |
| : |
| : |
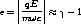
| (3.1) |
mit zweierlei Konsequenzen:
- kommt man mit
 -1 in die Nähe von 1, dann wird die Konvergenz zusehends schlechter,
-1 in die Nähe von 1, dann wird die Konvergenz zusehends schlechter,
- als Störungstheorie hat man einen hohen “handwerklichen” analytischen Aufwand zu
absolvieren, obgleich in diesem Falle in einer ästhetisch überaus befriedigenden Form, die
außerdem gut als symbolischer Algorithmus (
 z.B. in Reduce oder Mathematica
z.B. in Reduce oder Mathematica )
implementierbar ist
)
implementierbar ist
. Auch wenn die Reichweite der Aussage bei den von Weyssow angegangenen speziellen Problemen
etwas hinter dem Möglichen ( siehe die folgende Beschreibung des Bauerschen Ansatzes
siehe die folgende Beschreibung des Bauerschen Ansatzes )
zurückbleibt, ist doch zu bemerken, daß das Vorgehen an sich aus erkenntnistheoretischer Sicht
nahezu kanonisch erscheint. Anhang C erläutert dies etwas präziser.
)
zurückbleibt, ist doch zu bemerken, daß das Vorgehen an sich aus erkenntnistheoretischer Sicht
nahezu kanonisch erscheint. Anhang C erläutert dies etwas präziser.
3.1.2 Bauer-Mulser-Methode der gemittelten Lagrange-Funktion
3.1.2.1 Vorgehensweise
Das zentrale Thema der Diplom-Arbeit Dieter Bauers [Bau95] ist die Tragweite der Adiabasie-
Vermutung.
Er lotete in einem experimentellen Teil mittels numerischer Simulationis des geladenen Teilchens in
der elektromagnetischen Welle aus, in welchem Parameterbereich noch befriedigende
Übereinstimmung mit auf der Unterstellung beinahe-periodischer Bahnen basierenden analytischen
Rechnungen zu erzielen ist.
Der große theoretische Wurf ist die konsistente Beschreibung der Dynamik des Oszillationszentri aus
der Kenntnis der Dynamik des Teilchens im Rahmen des Lagrangeschen Dynamik-Paradigmas. Der
entscheidende Satz leitet aus der Lagrange-Funktioni für das Teilchen eine [“gemittelte”] für das
Oszillationszentrum her.
Sowohl die [computer-]experimentellen Ergebnisse als auch die theoretische Stabilitäts-
Analyse zeigen, daß die die bekannten Herleitungen stützende Voraussetzung der beinahe-
periodischen Bahn oberhalb eines Werts des Parameters  :=
:=  von etwa 0.3 bis 0.7
versagt.
von etwa 0.3 bis 0.7
versagt.
3.1.2.2 Kritik
Selbst wenn störungstheoretische Ansätze bis zu den Weihen der Weyssow-Balescu-schen
Arbeiten gelangen, bedingt doch der störungs-rechnerische Aspekt eine Komplexität,
die beginnt schwer kommunizierbar zu werden. Die Last zweier Drittel dieser
Komplexität hat Dieter Bauer für alle Zukunft von den Schultern der Community
genommen.3
Jede an Präzision darüberhinausgehende Kenntnis des Verhaltens des Einzelteilchens wird wohl nur
über ein weiteres Einbringen von Kenntnis über konkrete Bedingungen eines Einzelfalls zu erzielen
sein - sicherlich wird sich dabei auch ein gewisses Einbringen neuer handwerklicher Komplexität
nicht vermeiden lassen.
3.2 Kräfte auf makroskopische Media
3.2.1 Die Helmholtz-Schule der Makroskopiker
Helmholtz verfertigte bereits 1881 [Hel81], aufbauend auf Veröffentlichungen Thomsons und
Maxwells [Max73], §§104..107 eine Arbeit, in der er die Kräfte des elektrischen und magnetischen
Feldes auf die makroskopische Materie berechnete - in einer mit heutiger Denke leider recht
mühsam verständlichen Form. Wir werden weiter unten sehen, daß sein Ausdruck vor dem
Hintergrund des Wissens um den “richtigen” thermodynamischen Druck nach wie vor korrekt
ist.
Helmholtzs Arbeit hat im Laufe der Jahrzehnte manche Überarbeitung in
der Darstellung erfahren, so daß sie heute wesentlich leichter lesbar ist. Die
klarsten4
[mir bekannten] Darstellungen wurden von Panofsky und Phillips [PP55], Kap. 6-6, sowie Becker
und Sauter [BS69a], §35 und, mit etwas anderem Ansatz, von Landau und Lifschitz [LL85], §15
ff. gegeben:
3.2.1.1 Helmholtz, Panofsky & Phillips, Becker & Sauter
In diesen Werken wird die Bewegung eines dielektrischen Fluidi in einer Anordnung raumfester
Leiter untersucht. Die Änderung der Gesamtenergie der Anordnung bei diesem Prozeß wird
betrachtet als Volumenintegral über einerseits das Produkt aus der [unbekannten] lokalen
Kraftdichte mit der dortigen Verschiebung des Dielektriki und andererseits die Änderung der
Energiedichte des Feldes. Die lokale Verschiebung steht über die Massenerhaltung in Beziehung zur
materiellen Dichte. Durch Vergleich sich entsprechender Terminorum erhält man schließlich die
Kraftdichte in Abhängigkeit von Änderungen der Felder, der materiellen Dichte und der
Suszeptibilitäten.
3.2.1.2 Landau und Lifschitz
Der Weg, den Landau & Lifschitz in [LL85], §15 ff. beschreiten, führt über die Änderung der Dichte
der freien Energie bei einer infinitesimalen Scher-Dehnung eines Volumenelementi mit der
Randbedingung eines konstanten Potentials an den zur Dehnungsrichtung senkrechten
Oberflächen.
Will man diese Anordnung eines Volumenelementi tatsächlich aufbauen, so muß man, soll die
Potentialdifferenz der beiden gegenüberliegenden Seiten konstant bleiben, der Ladung, die diese
Potentialdifferenz erzeugt, ein Abfließen bei konstanter Spannung, d.h. mit Kopplung an ein
Ladungsbad, ermöglichen. Die bei diesem Vorgang durch die abfließende Ladung an der Umgebung
( dem Ladungsbad
dem Ladungsbad ) geleistete Arbeit
) geleistete Arbeit  W = U
W = U  q ist natürlich in der Energiebilanz zu
berücksichtigen, hier durch Rechnen mit einer Energiedichte, die nicht nur bezügl. der Wärme,
sondern auch der Ladung frei ist.
q ist natürlich in der Energiebilanz zu
berücksichtigen, hier durch Rechnen mit einer Energiedichte, die nicht nur bezügl. der Wärme,
sondern auch der Ladung frei ist.
3.2.2 Die Kelvin-Schule der Mikroskopiker
3.2.2.1 Penfield und Haus
Wesentlicher Punkt in Penfield’s und Haus’5
“Electrodynamics of Moving Media”, [PH67], ist das Herausarbeiten der Bedeutung
einer konsistenten Aufteilung eines abgeschlossenen Gesamtsystems in Teilsysteme, wenn
kontinuum-mechanische Fragestellungen anstehen.
Historie
Ausgangspunkt war ihre Unzufriedenheit mit dem nicht-enden-wollenden Zustand der Publikations-
Praxis, daß anscheinend widersprüchliche Ausdrücke für dieselben Phänomene oft nur nach
längerem Gelehrten-Streit zu identifizieren waren.
Abgeschlossene Teilsysteme
bieten ihrer [nachvollziehbaren] Auffassung nach ein geeignetes Mittel, die Vielzahl der möglichen
Darstellungen zu kanonisieren. Gleichzeitig geben sie ein zusätzliches Instrument zur Konsistenz-
Prüfung zur Hand:
Das Prinzip der virtuellen Leistung
ist der von ihnen entwickelte Algorithmus, den sie zur konsistenten Konstruktioni der Subsysteme
eines abgeschlossenen Systems nahelegen:
Für jedes nicht-abgeschlossene Teilsystem:
- Definieren einer Energiedichte
- Ausdrücken von (3.2a) in Terminis des tangentialen Bezugssystems
- Transformieren mit der gewünschten Zeit-Raum-Transformationi auf Labor-Koordinaten
- Ausführen aller anstehenden Ableitungen
- Eliminieren der Größen, die bei Setzen von
nicht verschwinden, mit Hilfe der das Subsystem beschreibenden Gleichungen
- Da
 jvk und vk,0 voraussetzungsgemäß unabhängig vari¨iert werden können, lassen sich T
und G Term für Term bestimmen.
jvk und vk,0 voraussetzungsgemäß unabhängig vari¨iert werden können, lassen sich T
und G Term für Term bestimmen.
- Aus läßt sich schließlich die Kraftdichte f auf dieses Subsystem bestimmen.
Ein abgeschlossenes System erfordert natürlich
.
3.2.2.2 De Groot und Suttorp
In der Kentwellschen Systematik unter die Spannungstensor-Formulierungen mit zeitabhängiger
Amplitudini (dort Abschnitt 3.3) einzureihen ist eine Arbeit von de Groot und Suttorp. In ihrem
Buch “Foundations of Electrodynamics” [GS72] fällt sozusagen en passant ein Ausdruck ab, der die
ponderomotorische Kraft auf ein Medium bestimmt.
Historie
De Groot hat 1969 in einer kleinen Studie [Gro69] vorgeführt, wie die Vakuum-Maxwellgleichungen
mathematisch sehr viel klarer als in der ursprünglichen Lorentz’schen Herleitung makroskopisiert
werden können. Auch in relativistischer Darstellung bereitet dies offensichtlich keine
Schwierigkeiten. Drei Jahre später war die weitere Arbeit so weit herangereift, daß ein sehr viel
ausführlicheres Buch [GS72] mit Suttorp zusammen veröffentlicht werden konnte.
Das Verfahren
Es geht, wie die ursprüngliche Herleitung durch Lorentz, von einer Zerlegung der
Ladungsverteilung in in sich stabile Ladungscluster ( Atome, Moleküle, Kristalle
o.ä.
Atome, Moleküle, Kristalle
o.ä. ) aus und liefert über eine Taylor-Entwicklung der Ladungsverteilung dieser
Cluster6
in mikroskopische (magnetische und elektrische) Multipol-Momenta und
die übliche thermodynamische Ensemble-Mittelung die makroskopischen
Maxwellgleichungen7.
) aus und liefert über eine Taylor-Entwicklung der Ladungsverteilung dieser
Cluster6
in mikroskopische (magnetische und elektrische) Multipol-Momenta und
die übliche thermodynamische Ensemble-Mittelung die makroskopischen
Maxwellgleichungen7.
Völlig analog bestimmt er aus der mikroskopischen Lorentz-Kraft-Gleichung die makroskopische
Kraft auf ein Medium, wobei auch die Wechselwirkung der einzelnen Ladungscluster
untereinander, in Abhängigkeit davon, wie sie im Phasenraum korreliert sind, Berücksichtigung
findet.
Kritik
De Groot und Suttorp setzen voraus, daß die Ladungscluster als stabile Gebilde erhalten bleiben
müssen. Systeme, in denen in nennenswertem Maße Ionisation und Rekombination eine Rolle
spielen, werden also hier nicht modelliert.
Wie ein einzelner Ladungscluster seine Ladungsverteilung und damit seine Multipol-Momenta im
Feld einstellt, wird nicht behandelt; die Ladungsverteilung wird zu einem bestimmten Zeitpunkt als
gegeben hingenommen. Insoweit ist die Theorie auch voll nichtlinear - Linearität wird oft erst
eingebracht, wenn man die Dynamik der mikroskopischen Multipol-Momentorum mit
linearen Differentialgleichungen modelliert. Das wird dann traditionell in der Theorie der
dielektrischen und magnetischen Suszeptibilitäten getan; siehe z.B. van Vleck 1932 [Vle32],
[Vle52].
Es wird nur zum Zwecke der Makroskopisierung ensemble-gemittelt - damit ist makroskopisch
weiterhin das gesamte zeitliche Spektrum der Kraft sichtbar. In den meisten Fällen werden
unsere Detektores nicht der vollen Frequenz des Lichtes folgen können ( sobald die
Nichtlinearität der Mediorum eine Rolle zu spielen beginnt, müßten sie auch noch den Oberwellen
folgen
sobald die
Nichtlinearität der Mediorum eine Rolle zu spielen beginnt, müßten sie auch noch den Oberwellen
folgen ), d.h. die unserer Detektorträgheit entsprechende Zeit-Mittelung respektive
Tiefpassfilterung auszuführen, steht samt der damit verbundenen Schwierigkeiten noch
aus.
), d.h. die unserer Detektorträgheit entsprechende Zeit-Mittelung respektive
Tiefpassfilterung auszuführen, steht samt der damit verbundenen Schwierigkeiten noch
aus.
Kapitel 4
Praeliminaria
4.1 Überblick
| Fi : | ponderomotorische Kraftdichte |
| n : | Teilchenzahldichte |
| q : | Ladung eines einzelnen Teilchens |
| m : | Masse eines einzelnen Teilchens |
 : : | Winkelfrequenz des E-Feldes |
| : |
| : |
| : |
| : |
| : |
 siehe z.B. Chen, Kap. 8, Gl. (8.39), [Che76]
siehe z.B. Chen, Kap. 8, Gl. (8.39), [Che76] ) hinaus.
) hinaus.
Der hiesige Ansatz folgt den Spuren der klassischen Suszeptibilitätstheorie und fügt einige der
besten [mir bekannten] Arbeiten zu einem einheitlichen Ganzen. Im einfachsten über
Einzelteilchen-Betrachtungen hinausgehenden Fall bringt die Gegenwart vieler Teilchen zwei neue
Phänomene:
- bei kleinen bis mittleren Licht-Intensitäten und geringen Photonen-Energien (
 solange
Ionisation nicht stattfindet
solange
Ionisation nicht stattfindet ) besteht die Target-Materie noch aus in sich stabilen
gebundenen Ladungsklumpen (
) besteht die Target-Materie noch aus in sich stabilen
gebundenen Ladungsklumpen ( Atome, Moleküle, Kristalle
Atome, Moleküle, Kristalle ). Die Bindung einer
Ladung läßt sie mit anderer Phasenlage1
auf ein anregendes Feld antworten als ein freies Teilchen. Von dieser Phase ist die Kraft
abhängig, die solch ein Oszillator im Feld erfährt. Das Maß, mit dem jeder einzelne
Teil-Oszillator eines Klumpens am Geschehen “teilnimmt”, kann durch sogenannte
Oszillatorstärken beschrieben werden, die quantenmechanisch oder phänomenologisch
zu bestimmen sind,
). Die Bindung einer
Ladung läßt sie mit anderer Phasenlage1
auf ein anregendes Feld antworten als ein freies Teilchen. Von dieser Phase ist die Kraft
abhängig, die solch ein Oszillator im Feld erfährt. Das Maß, mit dem jeder einzelne
Teil-Oszillator eines Klumpens am Geschehen “teilnimmt”, kann durch sogenannte
Oszillatorstärken beschrieben werden, die quantenmechanisch oder phänomenologisch
zu bestimmen sind,
- die einzelnen Ladungsklumpen erzeugen Felder, die wiederum auf die Nachbarklumpen
wirken. Das Feld am Ort eines Ladungsklumpens ist also nicht das Vakuumfeld [wie
beim Einzelteilchen], sondern das Superponat aus Vakuumfeld und dem von allen
anderen Ladungsklumpen des Systems verursachten.
In einer etwas realistischeren Modellierung der Welt wäre sicher noch das Spiel von Ionisationi und
Rekombinationi zu berücksichtigen. Dieses Maß an Realismo wird die vorliegende Arbeit jedoch
schuldig bleiben.
Das Verhalten teil-ionisierter Plasmen2
ist auf der Basis des vorliegenden Rahmens noch recht einfach zu beschreiben, indem man
Mischungen eingehender studiert.
4.2 Liminaria
4.2.1 klassisch oder relativistisch ?
Relativistische Effekte beginnen Berücksichtigung zu fordern, wenn die Energien einzelner [Sub-
]Systeme relativ zu deren Ruhmasse nicht mehr zu vernachlässigen sind. Im hier studierten
Szenario gewinnt dieses Kriterium zuerst für die Elektronen mit ihrer geringen Ruhmasse
Bedeutung.
Die “Bahn” eines einzelnen Elektrons ist im Rahmen hiesigen Modells darstellbar als Superponat
aus hydrodynamischer Geschwindigkeit, thermischer Geschwindigkeit seines Gast-Ladungsklumpens
sowie der Oszillations-Geschwindigkeit innerhalb dieses Ladungsklumpens. Eine relativistisch
werdende hydrodynamische Geschwindigkeit ist durch eine einfache “makroskopische” Lorentz-
Transformationem zu beschreiben. Sowohl relativistische Temperaturen als auch relativistische
Oszillations-Energien liegen aber so weit oberhalb der Dissoziations-Energien der als
Ladungsklumpen wohl meist in Frage kommenden Atome und Moleküle, daß das relativistische
Regime und das der stabilen Ladungsklumpen sich für praktisch relevante Fälle gegenseitig
ausschließen dürften.
Alle weiteren Betrachtungen werden sich daher hier auf den nichtrelatistischen Grenzfall
beschränken.
4.2.2 klassisch oder quantenmechanisch ?
| m : | Masse eines Elektrons |
   : : | Winkelfrequenz des Übergangs vom Zustand  in den Zustand in den Zustand  |
 : : | Winkelfrequenz des Treiberfeldes |
f  : : | Oszillatorstärke mit dem der Übergang vom Zustand  in den Zustand in den Zustand  beiträgt
beiträgt |
<  > : > : | Erwartungswert der Polarisationis des Atoms im Zustand  |
| : |
| : |
| : |
| : |

 meist nicht exakt
ausführbar, wiewohl die Gestalt von (4.2) unberührt zu bleiben scheint. (
meist nicht exakt
ausführbar, wiewohl die Gestalt von (4.2) unberührt zu bleiben scheint. ( siehe z.B. [BS63],
§§39..41
siehe z.B. [BS63],
§§39..41 ).
).
4.3 Thermodynamische Praeliminaria
Wir werden im Zuge der weiteren Rechnungen von mikroskopischen auf makroskopische Größen zu
schließen haben. Um den Fluß der Darlegungen später nicht zu stören, studieren wir zunächst
einige Brösel Thermodynamik.
4.3.1 Ensemble-Mittelung
| N : | Anzahl der Teilchen des betrachteten Systems |
| Rai : | Ort des a-ten Teilchens |
d : : | Phasenraumelement  ijadRaidRaj,0
ijadRaidRaj,0 |
| b : | mikroskopische Größe |
| B : | makroskopische Größe |
| C : | Basis-Körper des linearen Raumes der Funktionum b bzw. f |
| c : | c  C , d.h. es ist ein Skalar des linearen Raumes der Funktionum b bzw. f C , d.h. es ist ein Skalar des linearen Raumes der Funktionum b bzw. f |
| f : | Verteilungsfunktion, i.e. Wahrscheinlichkeit[sdichte], ein bestimmtes
Ensemble anzutreffen |
| : |
| : |
| : |
| : |
.
4.3.1.1 Additiones
vertauschen wegen der Distributivität der Multiplikationis mit der Verteilungsfunktioni und der
Linearität der Integrationis mit der Ensemble-Mittelung:
Auch
4.3.1.2 Skalar-Multiplikationes
vertauschen wegen
mit der Ensemble-Mittelung.
Daß schließlich auch
4.3.1.3 Differentiationes
nach Zeit und Ort mit der Ensemble-Mittelung vertauschen, ersehen wir folgendem Argument:
Die linke und die rechte in der Kette der folgenden Gleichheiten spiegeln schlicht die
Definitionem der Mittelwertbildung. Die mittlere ergibt sich aus der Tatsache, daß die
Wahrscheinlichkeit fd bei einer Transformationi der (Zeit und Orts)-Koordinate konstant bleibt.
bei einer Transformationi der (Zeit und Orts)-Koordinate konstant bleibt.

| (4.7) |
4.3.1.4 Reduzierte Verteilungsfunktiones, Korrelationes
| f1(t,R1,R1,0)
: | Einteilchen-Verteilungsfunktion, i.e. Wahrscheinlichkeit[sdichte],
irgendeines der Teilchen mit einer Geschwindigkeit R1,0 am Ort R1
anzutreffen |
| f2(t,R1,R1,0,R2,R2,0)
: | Zweiteilchen-Verteilungsfunktion, i.e. Wahrscheinlichkeit[sdichte],
irgendeines der Teilchen mit einer Geschwindigkeit R1,0 am Ort R1 und
ein anderes mit einer Geschwindigkeit R2,0 am Ort R2 anzutreffen |
| c2(t,R1,R1,0,R2,R2,0)
: | Zweiteilchen-Korrelationsfunktion |
 : : | Bezeichner einer Teilchensorte |
 : : | Bezeichner einer davon unterscheidbaren Teilchensorte |
| : |
| : |
| : |
| : |
Dies gibt Anlaß zur Definitioni sogenannter Ein- bzw. Zweiteilchen-Verteilungsfunktionum
. Letztere für den Fall zweier Teilchensorten  ,
,  unterscheidet sich von der Zweiteilchen-
Verteilungsfunktionibus f2
unterscheidet sich von der Zweiteilchen-
Verteilungsfunktionibus f2
 durch die andere Normierung. Oft benötigt man noch die sogenannte
Korrelationsfunktionem
durch die andere Normierung. Oft benötigt man noch die sogenannte
Korrelationsfunktionem
Ausführlichere Darlegungen zu reduzierten Verteilungsfunktionibus findet man in jedem besseren
Lehrbuch zur Thermodynamik, z.B. [Bal75], §3.1.
4.4 Kontinuum-mechanische Praeliminaria
| dV : | betrachtetes Volumenelement |
| dO : | Oberflächen-Element |
| F : | Kraft auf ein Volumenelement  |
| f : | Kraftdichte |
 ij : ij : | Spannungstensor i.e. Impulsstromdichte |
| : |
| : |
| : |
| : |
 Dichte der extensiven Größe
Dichte der extensiven Größe ) über das interessante
Raumgebiet. Der Vorgang der Integrationis über ein Raumgebiet wird in der Mathematik greifbar
gemacht, indem man - im Grenzwert betrachtet - das Integrationsgebiet in immer kleinere
Volumenelementa zerlegt, deren Beitrag man aufsummiert.
) über das interessante
Raumgebiet. Der Vorgang der Integrationis über ein Raumgebiet wird in der Mathematik greifbar
gemacht, indem man - im Grenzwert betrachtet - das Integrationsgebiet in immer kleinere
Volumenelementa zerlegt, deren Beitrag man aufsummiert.
Die Kraft auf ein einzelnes Volumenelement setzt sich aus zwei Anteilen zusammen:
- der Kraft auf sein Inneres
- der Summe der Kräfte auf seine Oberflächen
.
Während
4.4.1 die Kraft auf das Innere eines Volumenelementi
schlicht
ist, bedarf
4.4.2 der Kraft-Anteil auf die Oberfläche eines Volumenelementi
einer etwas feineren Betrachtung:
Wie man in Abbildung 4.1
sieht, wirken auf die Oberflächen-Elementa dOb
- an der Stelle x die Kraft F(x) und
- an der Stelle x+dx die Kraft F(x+dx)
. Die Impulsströme, die die jeweiligen Oberflächen-Elementa passieren, sind die Quotienten
.
Die Kraft, die über die beiden gegenüberliegenden Oberflächen-Elementa dOj auf das
Volumenelement insgesamt wirkt, ist also
. Letztere Umformung geht auf das Konto einer Taylor-Entwicklung von  um x in j-Richtung,
wobei k formal als neuer freier Index eingeführt wurde, obschon er mit j übereinstimmt.
um x in j-Richtung,
wobei k formal als neuer freier Index eingeführt wurde, obschon er mit j übereinstimmt.
Auch Oberflächenkräfte auf die einzelnen Volumenelementa üben also auf diese Kräfte aus, die
ihrem Volumini proportional sind, mithin von der [Kraft-]Dichte
. Wir haben bisher nur den Kraftbeitrag vermöge der einzelnen Raumrichtung j betrachtet.
Natürlich kann man für j jede der drei Raumrichtungen setzen und man muss es auch, um die
Beiträge der Kräfte auf die vier Oberflächen der anderen beiden Raumrichtungen mitzuzählen. Die
letzte Gleichung ist also durchaus im Sinne der Einsteinschen Summierkonventionis zu lesen, der ihr
so insgeheim untergeschoben wurde.
4.4.3 Granulare Media
Im Falle eines Medii, das nicht wirklich homogen ist, sondern nur im Limes einer immer feiner
granularen Konsistenz betrachtet wird, führt das Zerlegen in Volumenelementa zu Modellierungs-
Artefakten, die folgend am Beispiel des Multipol-Fluidi beschrieben seien:
4.4.3.1 Die Kinderschaufel
Fände der Prozeß des Aufteilens in Volumenelementa tatsächlich nur so statt, daß die einzelnen
Granula des Medii unzertrennt blieben, so wie eine Kinder-Schaufel im Sandkasten beim
Stich in den Sand die einzelnen Sandkörner unversehrt läßt, dann wäre das Integral über
das gesamte Integrationsvolumen ohne weiteres gleich der Summe über die einzelnen
Volumenelementa ( Granula
Granula ).
).
4.4.3.2 Die Guillotine
Nun fährt der Mathematiker aber mit der ganzen Schärfe seiner mathematischen Trennebenen
einem Fallbeil gleich durch das Medium, ohne daß ein zufällig gelagertes Granulum die Wahl hätte,
sich in Gänze auf die eine oder andere Seite der Trennebene zu schlagen. Man hat dann sorgfältig
den [Oberflächen-]Beitrag zertrennter Granulorum zu bilanzieren - ein lästiges Artefakt, einzig
geboren aus der Willkür des Zerteilens des Integrationsgebiets.
4.4.4 Beispiel: elektrische Kräfte auf ein Multipol-Fluidum
4.4.4.1 Die Kinderschaufel
Wenden wir diese Erkenntnis auf den Fall unseres Multipol-Fluidi an, dann ist die Kraft auf ein
bestimmtes Raumgebiet im Falle des mit der “Kinder-Schaufel” zerlegten Integrationsgebiets, bei
dem kein Multipol zerteilt wird, einfach der Summe der Kelvin-Kräfte auf die einzelnen
Multipole.
4.4.4.2 Die Guillotine
Wollten wir im Falle, daß uns ein Mathematiker unser Integrationsgebiet mit der Guillotine zerlegt
hat, die Kraft auf ein Volumenelement bestimmen, dann setzte sich diese aus drei Anteilen
zusammen:
- der Kelvin-Kraft des äußeren Feldes auf die unzerschnittenen Multipole im Innern des
Volumenelementi,
- dem Kraftanteil des Feldes auf die im Innern des Volumenelementi verbliebenen Multipolfragmenta (
 meistens
wird dies die Summe der Lorentz-Kräfte auf die einzelnen Ladungen sein - jedenfalls
solange man nicht davon beseelt ist, die auch noch zerhacken zu wollen
meistens
wird dies die Summe der Lorentz-Kräfte auf die einzelnen Ladungen sein - jedenfalls
solange man nicht davon beseelt ist, die auch noch zerhacken zu wollen )5
)5
- der Kraft, die die äußeren Multipolfragmenta auf die inneren ausüben
.
Die ganze Fragwürdigkeit des unpragmatischen Standpunkts, den man damit einnimmt, wenn man
Multipole zertrennt, zeigt sich, wenn man sich gewärtigt, daß die Kräfte, die die einzelnen
Bestandteile eines Multipols aufeinander ausüben, in den meisten Fällen gar nicht observabel
sind.
Die Konsequenzen aus dieser Einsicht können nur lauten:
- die Literatur befrage man sehr genau nach der Wahl der Zerlegung und den
Konsequenzen für die Berechnung von Oberflächenkräften,
- wir nehmen die Kinderschaufel, d.h. die Lage des Entwicklungszentri eines Multipols
entscheidet über die Zugehörigkeit zu “seinem” Volumenelemento,
- wollten wir einen Feststoff untersuchen, müssten auch wir wohl zur Guillotine greifen,
denn dann dürfte sich schwerlich eine Zerlegungsmöglichkeit auf einer mesoskopischen
Ebene finden lassen, die nicht den gesamten makroskopischen Körper umfaßt, der dann
die Rolle des “Multipols” spielt
.
4.4.5 Die Wahl der Systemgrenzen
Auch bezüglich der Entscheidung, welchen Anteil der Kraft man als Volumenkraft und welchen man
als Oberflächenkraft betrachtet, ist man weitgehend ungebunden.
Vergegenwärtigen wir uns dies am Beispiel der Kräfte des elektrischen Feldes auf Ladungen:
4.4.5.1 Volumenkräfte
Betrachtet man das Feld als nicht zum System gehörig, dann greift es gleichsam an allen
Systemgrenzen vorbei in das Volumenelement hinein und wirkt auf die dort plazierten
Ladungen. Bei dieser Sicht der Dinge hat man sich dafür entschieden, die Kraft, die vermöge
der Wechselwirkung des Feldes auf die Ladungen zustandekommt, als Volumenkraft zu
betrachten.
Noch anschaulicher wird die Sache vielleicht, wenn man das Feld in Gestalt von Photonen
verkörpert sieht. Ein Photon passiert dann unregistriert die Oberfläche und erst, wenn
es zur Wechselwirkung mit einer Ladung im Innern kommt, wird sein Impulsübertrag
gezählt.
4.4.5.2 Oberflächenkräfte
Betrachtet man das Feld hingegen als zum System gehörig, dann sieht man es die Oberfläche
passieren, und der Anteil des Feldes, der im Innern des Volumenelementi mit einer Ladung zur
Wechselwirkung kommt, wird wegen der Coulombgleichung (5.1a) auf der gegenüberliegenden
Oberfläche nicht wieder heraustreten. Man ordnet also auch dem Feld selbst eine Spannung,
i.e. einen Impulsstrom zu, der schon beim Passieren der Oberfläche bilanziert wird.
Im Photonenbild heißt das: man zählt den Impuls des Photons just in dem Momento, in dem es die
Grenzen des Volumenelementi überschreitet.
Kapitel 5
Felder
5.1 Die Maxwell-Gleichungen
sind natürlich eine weitere [nicht ganz so kleine]
Vorbereitung1
auf die folgenden Betrachtungen über Kräfte.
| e : | ein Lichtgeschwindigkeitel des mikroskopischen elektrischen Feldes |
| b : | mikroskopisches magnetisches Feld |
| d : | mikroskopische dielektrische Verschiebung |
| h : | mikroskopische magnetische Induktion |
| Ra : | Ort des Teilchens “a” |
| qa : | Ladung des Teilchens “a” |
 a(n) : a(n) : | elektrisches Multipol-Moment n-ter Stufe des Teilchens “a” |
 a(n) : a(n) : | magnetisches Multipol-Moment n-ter Stufe des Teilchens “a” |
 : : | atomare freie Ladungsdichte |
| j : | ein Lichtgeschwindigkeitel der atomaren freien Stromdichte |
| p : | atomare Polarisation |
| m : | ein Lichtgeschwindigkeitel der atomaren Magnetisierung |
| : |
| : |
| : |
| : |
| : |
5.1.1 mikroskopisch
lebt man im Vakuo. Entsprechend sehen die Feldgleichungen aus:
5.1.2 atomar
| rbd : | Ort des Teilchens “bd” relativ zum Zentro des Ladungsklumpens “b” |
| : |
| : |
| : |
| : |
 e.s. in
praxi Atome, Moleküle, Kristalle
e.s. in
praxi Atome, Moleküle, Kristalle ), dann kann man die Maxwell-Gleichungen umschreiben, indem
man
), dann kann man die Maxwell-Gleichungen umschreiben, indem
man
- ersetzt:
die Nummer a jeder einzelnen Ladung
durch ein 2-Tupel bd mit
b: Nummer des Klumpens
d: Nummer innerhalb des Klumpens
und
- in eine Taylor-Reihe entwickelt die Ladungsverteilung innerhalb jedes einzelnen
Ladungsklumpens [mit der Nummer b] um einen geeigneten Entwicklungspunkt Rb (
 Schwerpunkt von Ladung, Masse, o.ä.
Schwerpunkt von Ladung, Masse, o.ä. ) mit dem Parameter rbd
) mit dem Parameter rbd
. Die bisher bei Ra erscheinende Ladungqa findet sich nun also als qbd bei Rb + rbd.
Die Maxwell-Gleichungen sehen nun nicht mehr ganz so bekannt
aus2,3:
.
Wir trachten ja in diesem Abschnitt danach, die Maxwell-Gleichungen in die bekannte Materie-
Form zu überführen und setzen - jeweils den nullten und die höheren Terminos der Taylor-
Entwicklung separierend - deshalb zunächst
und
und finden Gleichung (5.3a) schon wieder etwas einfacher: . Genauso setzt man
und
, womit sich schließlich auch Feld-Gleichung (5.3b)
vereinfacht4
und zwar zu
.
Nun ist es keine große Kunst, unliebsame Terminos in neudefinierten Variablen verschwinden zu
lassen5;
da unser gerade geschnürtes Päckchen aber etwas größer war, würdigen wir p und m noch eines
genaueren Blickes, der uns die Darstellung auf einer Ebene intermediärer Komplexität bescheren
wird.
Definieren wir, wie üblich, die elektrischen Multipol-Momenta
und magnetischen Multipol-Momenta
der d-ten Ladung des b-ten “Atoms”,
bzw. unddes ganzen “Atoms” b,
dann beschert uns dies, wie versprochen, die atomare Polarisationem p und atomare
Magnetisierung m in Terminis der elektrischen Multipol-Momentorum  und der magnetischen
Multipol-Momentorum
und der magnetischen
Multipol-Momentorum 
.
So erhält man schließlich
, bzw., wenn man, wie üblich
setzt,
schon fast in bekannter, freilich noch nicht ganz makroskopischer, Gestalt. Dazu fehlt noch die im
nächsten Abschnitt durchgeführt werdende Ensemble-Mittelung, die die Gleichungen von ihrer
jetzigen “atomaren” Form auf eben makroskopische hieven wird.
5.1.3 makroskopisch
| Ei : | ein Lichtgeschwindigkeitel des makroskopischen elektrischen Feldes |
| Bi : | makroskopisches magnetisches Feld |
| Di : | makroskopische dielektrische Verschiebung |
| Hi : | makroskopische magnetische Induktion |
| P : | makroskopische freie Ladungsdichte |
| Ji : | ein Lichtgeschwindigkeitel der makroskopischen freien Stromdichte |
| Pi : | makroskopische Polarisation |
| Mi : | ein Lichtgeschwindigkeitel der makroskopischen Magnetisierung |
| : |
| : |
| : |
| : |
Aus den Gleichungen (5.17) erhält man so6
. Da wegen (4.7) auch (Zeit- und Orts-)Ableitungen mit der Mittelbildung vertauschen, kann man
schreiben
, bzw., den makroskopischen Größen jeweils eigene Zeichen
spendierend,
.
Analog zu (5.18) mag man
setzen und erhält die Maxwell-Gleichungen schließlich in der gewohnten makroskopischen Form
.
F
eld im Medio]
5.2 Das [wirksame] Feld im Medio
5.2.1 Ein Beispiel: der Plattenkondensator
 m : m : | Flächen-Ladungsdichte auf der Oberfläche x = xm, m  {s,t,u,v} {s,t,u,v} |
 : : | dielektrische Suszeptibilität |
| : |
| : |
| : |
| : |
Dabei befinden sich auf den Kondensatorplatten ( d.h. bei xs und xv
d.h. bei xs und xv ) und auf den
Oberflächen des Dielektriki (
) und auf den
Oberflächen des Dielektriki ( d.h. bei xt und xu
d.h. bei xt und xu ) die tatsächlichen Flächen-Ladungsdichten
) die tatsächlichen Flächen-Ladungsdichten
, wobei in dieser Skizze, mit der üblichen Definitioni von
,  = 1 ist, d.h.
= 1 ist, d.h.  t = -1/2
t = -1/2  s.
s.
Vorausgesetzt, die ganze, hier skizzierte Konfiguration befinde sich im feldfreien Raum,
dann liefert die Integration der Maxwell-Gleichung (5.23a) für die Felder an den Orten
, d.h. das Feld im Innern des Dielektriki wird durch die an seiner Oberfläche heraustretenden
Polarisationsladungen abgeschirmt - im Falle dieses Beispiels auf die Hälfte.
5.2.2 Ladungsanhäufungen
Selbstverständlich sorgt jede Ladungsanhäufung, sei es eine freier Ladungen
oder auch eine durch Divergenzen der Polarisationis, für zusätzliche
Felder7, die einem
möglichen äußeren8
Feld überlagert sind.
5.2.2.1 Abschirmung
Kommen diese Ladungsanhäufungen und die hierherrührenden Felder erst als Systemantwort auf ein
äußeres Feld zustande, dann spricht man auch oft von Abschirmung.
In diesem Werk wird dem Begriff “Abschirmung” keine ausgezeichnete Bedeutung zukommen: im
Rahmen einer linearen Theorie ist alles über den Mechanismum der Superpositionis zu
verstehen.
Will man die Verhältnisse
5.2.3 am Orte eines Ladungsklumpens
studieren, dann simuliert man gerne eine Konfigurationem als
befände sich dieser Klumpen im Vakuo, indem man den Einfluß aller anderen Teilchen durch ein
Feld subsumiert. Das durch alle anderen Teilchen erzeugte Feld ist aber nicht das gesamte
Feld, sondern eben das gesamte Feld abzüglich des vom untersuchten Klumpen selbst
erzeugten.
5.2.3.1 Clausius-Mosotti
Die Bestimmung dieses Feldes ist Gegenstand einer Rechnung, deren Grundlagen Mosotti 1836
[Mos36] legte, indem er Moleküle als leitende Kugeln modellierte, und die man in modernerer
und auch konsistenterer Form z.B. in Becker und Sauter [BS69b], §19 nachvollziehen
kann.
Dabei modelliert man das Dielektrikum durch ein homogen polarisiertes Kontinuum mit kugelförmigem
Loch9.
In Praxi subtrahiert man von einem massiven Kontinuo eine kleine dielektrische Kugel gleicher
Polarisationis, von der man ja weiß, daß das Feld in ihrem Innern homogen und von der Stärke
ist. Strebte man eine auch den allgemeinen Fall angemessen modellierende Konfigurationem an,
dann müßte man die Granularität des Medii in Personae der dem Ladungsklumpen nächstgelegenen
“Kollegen” berücksichtigen, jedoch erweist sich, daß dies nur für sehr unsymmetrische
Fälle10
notwendig ist.
Da sich das Feld im gelochten Kontinuo und das Feld in der dielektrischen Kugel zum homogenen
E summieren, muß das Feld im Loch
sein.
5.2.3.2 Lorenz-Lorentz
H.A. Lorentz [Lor80a] und L. Lorenz [Lor80b] zeigten beide 1880 - vermutlich unabhängig
voneinander -, daß dieses Ergebnis auch für den Fall zeitabhängiger Felder gültig bleibt. Eine
modernere Darstellung findet man auch wieder z.B. bei Becker und Sauter [BS69b], §24. Etwas
überraschend ist hierbei die Tatsache, daß sowohl der Feldgradient um die Lorentz-Kugel als auch
die Retardierung vom umgebenden Medio zum Aufpunkt hin, das Ergebnis angeblich nicht
modifizieren. Bei der Herleitung selbst ist indes doch ein deutlich sorgfältigeres Vorgehen
vonnöten.
Kapitel 6
Kräfte
| Rb : | Ort des Zentri des Ladungsklumpens [, alias “Atoms”] “b” |
| Rbd : | Ort des d-ten Teilchens des b-ten Ladungsklumpens |
| rbd : | Ort des d-ten Teilchens des b-ten Ladungsklumpens relativ zum
Zentrum des Ladungsklumpens “b” |
 bi : bi : |  |
| qbd : | Ladung des d-ten Teilchens des b-ten Ladungsklumpens |
| Eext : | externes elektrisches Feld |
| ecmi(t,Rbd) : | elektrisches Feld am Ort der d-ten Ladung des b-ten Atoms ohne das Selbst-
Feld des Atoms “b” |
| Bext : | externes magnetisches Feld |
| bcmi(t,Rbd) : | magnetisch Feld am Ort der d-ten Ladung des b-ten Atoms ohne das Selbst-
Feld des Atoms “b” |
| fb : | Kraft auf das Atom “b” |
| fbext : | auf das externe Feld zurückzuführende Kraft auf das Atom “b” |
| fbaltshort : | kurzreichweitiger Anteil der Kraft, die die von den anderen Atomen
verursachten Felder auf das Atom “b” ausüben |
| fbaltlong : | langreichweitiger Anteil der Kraft, die die von den anderen Atomen
verursachten Felder auf das Atom “b” ausüben |
| Fshort : | kurzreichweitiger Anteil der Kraftdichte |
| Flong : | langreichweitiger Anteil der Kraftdichte |
| : |
| : |
| : |
| : |
6.1 Ein kleines Beispiel: der Dipol
| R : | Ort des Zentri des Dipols |
| r : | Ort der Ladung +q relativ zur Ladung -q |
| f + q : | Kraft auf die Ladung +q |
| f - q : | Kraft auf die Ladung -q |
| p : | Moment des Dipols -q -- +q |
| : |
| : |
| : |
| : |
| : |
Der Dipol bestehe aus den beiden Ladungen -q an der Stelle R -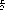 und +q an der Stelle
R +
und +q an der Stelle
R +  :
:
Die Kraft auf den ganzen Dipol ist die Summe der Kräfte auf die einzelnen Ladungen
.
Entwickelt man die Felder um R und berücksichtigt nur lineare Glieder, erhält
man1
bzw., wenn man wieder qr =: p einsetzt
.
Bereits dieser einfache Fall zeigt drei Terminos, die wir auch in ausführlicheren Rechnungen
wiederfinden werden:
- die elektrische Kelvin-Kraft
- eine magnetische Kelvin-Kraft
- eine Kraft, die man als “Dipol-Hall-Kraft” bezeichnen könnte
.
6.2 mikroskopisch
Auf die d-te Ladung des b-ten Atoms wirkt die Kraft
.
Am Ort der d-ten Ladung des b-ten Atoms sehen wir die Felder
. Hierbei beschreibt Term (6.5a) das externe elektrische Feld
, Term (6.5b) die von den Elektronen aller anderen Atome ( c
c b
b ) erzeugten Felder
, Term (6.5c) die von allen anderen (
) erzeugten Felder
, Term (6.5c) die von allen anderen ( e
e d
d ) Elektronen des eigenen Atoms erzeugten Felder
und Term (6.5d) das externe magnetische Feld, jeweils mit der retardierten Zeit
) Elektronen des eigenen Atoms erzeugten Felder
und Term (6.5d) das externe magnetische Feld, jeweils mit der retardierten Zeit
.
Die auf Ladungsbewegungen zurückzuführenden Beiträge zum Magnetfeld vernachlässigen wir in
unserer nichtrelativistischen Theorie wegen Rcf,0 « 1.
6.3 atomar
Unter dem Ort des Atoms b verstehen wir fürderhin den
.
Da Kräfte innerhalb eines Atoms nun ohnehin nicht observabel sind -- ein Atom vielmehr
in diesem Rahmen, gleichviel ob klassisch oder quantenmechanisch, als Multipol-
Oszillator beschrieben sei -- und für die Bestimmung der Kraft auf das Atom als
Ganzes2
auch gänzlich bedeutungslos, können wir den sie vermittelnden Feldanteil weglassen
und definieren das für seine Wirkung auf das ganze Atom b einzig bedeutsame Feld
.
Auf das Atom b wirkt insgesamt die Lorentz-Kraft
. Setzt man hier die Felder (6.10) ein, erhält man mit
, wobei (6.12a) den Kraft-Beitrag auf das Atom b in einem äußeren Feld Eexti(t,Rb), Bextj(t,Rb)
beschreibt und (6.12b) den von den Nachbaratomen herrührenden Felder verursachten,
.
6.3.1 Anteil vermöge des externen Feldes
Entwickelt3 man die
Felder (6.5) um Rb,4
dann wird (6.12a) zu
.
Einsetzen der elektrischen Multipol-Momentorum (5.14) mit (5.12) und der magnetischen Multipol-
Momentorum (5.15) mit (5.13) liefert zunächst
. rbdj,0 ist nun aber keine observable Größe, sondern steht vielmehr in direkter Relationi zu  j,
was Anlaß gibt, (6.15) noch etwas umzuschreiben.
j,
was Anlaß gibt, (6.15) noch etwas umzuschreiben.
Um dies ergonomisch zu bewältigen, formulieren wir zunächst folgenden
Beweis:
Siehe Anhang B.1.
_
, kraft dessen wir (6.15) schließlich in folgender Form finden
.
6.3.2 Anteil vermöge der Felder der Nachbaratome
Im allgemeinsten aller Fälle ergibt man sich einer gewissen Hilflosigkeit und stellt den von den
Feldern der Nachbaratome verursachten Kraftanteil (6.12b) schlicht in den Lösungen
der Coulombgleichung (5.1a) dar: . Man kann nun auch hier, analog zum vorherigen Abschnitt, das Feld um Rb in eine
Taylor-Reihe entwickeln und erhält für die von den Nachbaratomen verursachten Kräfte
.
6.3.3 Reichweite
6.3.3.1 kurzreichweitige Kräfte
Außerhalb des Konvergenzgebiets5,
steigert man seine Hilflosigkeit, indem man vom exakten Ausdruck (6.19) den eben errechneten
Unfug der dann vagabundierenden Taylor-Entwicklung (6.20a) wieder subtrahiert und so die
kurzreichweitige Kraft
definiert.
6.3.3.2 langreichweitige Kräfte
Mit dem Abspalten des kurzreichweitigen Kraftausdrucks (6.21) hat man sich der wenig greifbaren
Domäne der nicht-mehr-konvergierenden Taylor-Entwicklung entledigt und definiert die greifbarere
Kraft
, die man nun mit (6.10), (6.14) und (6.20a) schreiben kann und dann abarbeiten als hätten wir Abschnitt 6.3.1 vor uns als ein generisches Script
mit zwei Parametern, die dort Eexti(t,Rbd), Bexti(t,Rbd) gesetzt waren und jetzt ecmb(t,Rbd),
bcmb(t,Rbd).
So ergibt sich die langreichweitige Kraft dann völlig analog zu
, bzw., wenn man die Felder wieder explizit notiert,
.
6.3.4 Kraftdichte auf ein Ensemble von Atomen
Im gesamten bisherigen Abschnitt 6.3 wurde die Kraft auf das b-te Teilchen errechnet. Aus einer
weniger lokalen Perspektive auf das Medium interessiert aber vielmehr eine Kraftdichte in
Abhängigkeit vom Ort, die in Gegenwart eines ganzen Ensembles von Atomen auf dieses wirkt:
.
Die Dichte langreichweitiger Kräfte flong(t) wird so mit der im vorherigen Abschnitt dargestellten
entsprechenden Kraft fblong(t)
.
Der Rest dieses Abschnitts ist nun - völlig analog dem Vorgehen bei der Makroskopisierung der
Felder in Kapitel 5 - den Ersetzungen
gewidmet.
Für die Felder sind die Substitutiones (6.28a), (6.28b) rein syntaktisch. In deren Folge sind
jedoch die Differentialoperatores der Taylor-Entwicklung ebenfalls umzusetzen und zwar
gemäß (5.2).
6.3.4.1 Lorentz-Kelvin-Anteil auf den Atom-Strom
Die erste Zeile von (6.27) wird mit
und (5.7) zunächst zu
. Mit den ersten drei Terminis könnten wir in dieser Form zufrieden sein. Jedoch bedarf der
letzte noch der restlosen Ausführung der Summe über alle Atome ( also den Atom-
Indicem “
also den Atom-
Indicem “ ”
” ). Zielvorstellung der weiteren Umformungen wird die Interpretation der
“störenden” Atom-Geschwindigkeit
). Zielvorstellung der weiteren Umformungen wird die Interpretation der
“störenden” Atom-Geschwindigkeit  im Rahmen einer totalen zeitlichen Ableitung
sein. Mit dieser Perspektive schlüsseln wir den ganzen Term mit der Vektor-Identität
noch
etwas auf.
im Rahmen einer totalen zeitlichen Ableitung
sein. Mit dieser Perspektive schlüsseln wir den ganzen Term mit der Vektor-Identität
noch
etwas auf.
Auch den vorletzten Term stellen wir mit
zu um. An dieser Stelle ist es, vor dem Hintergrund vielfältiger Irritationum in der Welt der Literatur
zu diesem Thema, Zeit für ein klärendes Wort: die Kelvin-Kraft präsentiert sich in ihrer
“mikroskopischen Form” wie die linke Seite von (6.33). Ganz offensichtlich ist diese mit der
“makroskopischen Form” in Gestalt des ersten Termini der rechten Seite von (6.33) identisch,
wenn das magnetische Feld “ ” sich nicht mit der Zeit ändert. Bei zeitabhängigem
Magnetfeld ist sehr wohl darauf zu achten, wie der Kelvin-Term verjüngt wird. Hier hätte eine
ausreichend explizite Schreibweise dem Leser wissenschaftlicher Literatur sicher manch’ irrige
Interpretationem erspart7.
” sich nicht mit der Zeit ändert. Bei zeitabhängigem
Magnetfeld ist sehr wohl darauf zu achten, wie der Kelvin-Term verjüngt wird. Hier hätte eine
ausreichend explizite Schreibweise dem Leser wissenschaftlicher Literatur sicher manch’ irrige
Interpretationem erspart7.
6.3.4.2 Lorentz-Kelvin-Anteil auf intra-atomare Ströme
Die zweite Zeile von (6.27) wird mit
und (5.16c) zu
.
6.3.4.3 Totum Virium
Mit der Bemerkung, daß die Summe (6.35f).1 + (6.33) + (6.31) gerade
ist, wird nun die gesamte langreichweitige Kraft
.
6.4 makroskopisch
6.4.1 Die Massenbilanz
Die makroskopische Massendichte sei
definiert.
Deren zeitliche Änderung ist
, wegen (4.7) und
.
Mit der Massenstromdichte
definiert man die lokale hydrodynamische Geschwindigkeit
.
Wegen
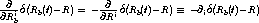
| (6.43) |
kann man (6.39) in die Massen-Kontinu¨itätsgleichung
umformen.
6.4.2 Die Impulsbilanz
Die Kraftdichte aller anderen Subsysteme auf das Trägheits-Subsystem ist die hydrodynamische
Impulsstromdichte abzüglich der auf Dichte-Zunahme zurückzuführenden Impulsstromdichte:
.
Wir werden in diesem Unterkapitel das zweifellos wünschenswerte Ziel, einen Erhaltungssatz für die
Impulsstromdichte zu formulieren, nicht bis zum Ende durchführen. Dennoch werden wir, in stiller
Vorbereitung auf diese Form, zur ebengenannten Kraftdichte auf das Trägheits-Subsystem die auf
Dichte-Zunahme zurückzuführende Impulsstromdichte addieren und in den folgenden Formeln
die zeitliche Ableitung des Trägheitsanteils der Impulsstromdichte auf die linke Seite
stellen.
Diese ist in unmittelbarer Folge von Definitioni (6.41a) und dann mit einigen Umformungen
.
Mit der Geschwindigkeits-Fluktuationi8
, der Bemerkung, daß
, dem kinetischen Druck sowie den makroskopischen lang- und kurz-reichweitigen Kraftdichten
erhält man hieraus die Impulsbilanz , also
.
Wegen der Vertauschbarkeit von Ensemble-Mittelung und Addition ( siehe (4.5)
siehe (4.5) ) kann man die
Ensemble-Mittelung “ausmultiplizieren”:
) kann man die
Ensemble-Mittelung “ausmultiplizieren”:
.
Unter Vernachlässigung von Fluktuationibus9
wird hieraus schließlich
und mit den Vereinbarungen (5.22) für die makroskopischen Größen
.
An dieser Stelle ist man nun an einer Wegesgabel angelangt und hat
sich zu entscheiden, ob man sich weiter auf de Groots Pfade begeben
will10,
aus der Situationi weitgehender Unkenntnis des konkreten Medii das Maximum theoretischer
Aussagefülle zu knautschen oder hier folgend in die Niederungen praktisch relevanter
Konfigurationum, und Media studiert, die deterministisch auf externe Felder antworten.
6.5 Media mit P = P(E)
| D : | Raumbereich, in dem diskret gerechnet wird |
| K : | Raumbereich des Kontinui |
 K : K : | Rand des Kontinui |
| ecm(t,Rb) : | Feld am Ort des Atoms b ohne dessen Selbstfeld; in der Literatur auch oft
“wirksam Feld” genannt |
| : |
| : |
| : |
| : |
| : |
Solange wir die Domäne modellieren, in der die Ladungsklumpen als lineare Oszillatores zu beschreiben
sind, wird aus der funktionalen Abhängigkeit ec-s von Eext eine einfache Proportionalität mit einem
Faktori11
fc
, das Feld als Ganzes also
.
6.5.1 Eine diskret-kontinu¨ierliche CM-Verallgemeinerung
Nun sind nur für überschaubare Teilchenzahlen derartige Summen ein angemessenes Mittel; mit
größer werdenden Teilchenzahlen andererseits werden Mittelungen immer genauer, und eröffnen uns
so die Domäne der Kontinuorum.
Ein in vielen Fällen sehr gutes Modell sieht dann so aus, daß man Felder unmittelbarer
Nachbarklumpen durch Summieren á la (6.56b) gewinnt und jenseits eines gewissen Horizonts
(
 K
K
 ) über via [thermodynamischer] Mittelung kontinu¨ierte Zellen des Medii integriert. Insbesondere
in Mediis mit Nahordnung [wie Kristallen und Gläsern] sind die Summen leicht ausführbar. Eine
geschickte Wahl der Horizont-Oberfläche wird meist durch die geometrische Symmetrie des
Medii nahegelegt.
) über via [thermodynamischer] Mittelung kontinu¨ierte Zellen des Medii integriert. Insbesondere
in Mediis mit Nahordnung [wie Kristallen und Gläsern] sind die Summen leicht ausführbar. Eine
geschickte Wahl der Horizont-Oberfläche wird meist durch die geometrische Symmetrie des
Medii nahegelegt.
6.5.2 Das “wirksame” Feld am Ort eines Atoms
mit der Nummer “b” setzt sich in unserem diskret-kontinu¨ierlichen Falle aus den vier Terminis
zusammen. Dabei ist
- Term (6.59a) der Beitrag des externen Feldes
- Term (6.59b) der Beitrag des Randes des Kontinui
- Term (6.59c) der Beitrag von Polarisations-Inhomogenitäten des Kontinui
- Term (6.59d) der Beitrag der einzelnen Nachbaratome im Bereich der diskreten
Modellierung, den man auch in der Form (6.58) hätte schreiben können
.
Der den
6.5.2.1 Beitrag der Horizont-Oberfläche
 beschreibende Term (6.59b) kann noch anschaulicher umgeformt werden, wenn man bemerkt,
daß
beschreibende Term (6.59b) kann noch anschaulicher umgeformt werden, wenn man bemerkt,
daß  jPj einer Ladungsdichte
jPj einer Ladungsdichte 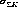 entspricht:
entspricht:
Just an der Horizont-Oberfläche springt die Polarisation von P = lim(R K)
K)
 K P(R) auf
P = 0.
K P(R) auf
P = 0.
Coulombgleichung (5.23a) zeigt zunächst
einerseits12,
daß diesem Sprung der Polarisationis ein Sprung des elektrischen Feldes in entgegengesetzt gleicher
Höhe entsprechen muß:
.
Stellt man sich andererseits --
abkürzend -- auf den Monopol-Standpunkt der Maxwell-Gleichung (5.1a) , bzw. in makroskopischer Form , dann sieht man per Integrationem über die Normale der Horizont-Oberfläche unmittelbar, daß die
auf unkompensierte Polarisationsladungen zurückzuführende Flächen-Ladungsdichte auf der
Horizont-Oberfläche gerade ist.
Term (6.59b) zeigt sich damit in der etwas eingängigeren Form
.
Im
-
symmetrischer Mediorum]
6.5.2.2 Fall lokal kugel[i.e. SO(3)]-symmetrischer Mediorum
ist die Horizont-Oberfläche  K eine Kugel.
K eine Kugel.
R, , , : : | Tripel der Polarkoordinaten |
| dO : | infinitesimales Element der Horizont-Oberfläche |
| : |
| : |
| : |
| : |
| : |
.
In Polarkoordinaten ist die Ladungsdichte auf der Kugeloberfläche [, da das Feld in der Kugel homogen
ist13,]
, und das Oberflächen-Element . Mithin ist der Beitrag der nicht-neutralisierten Polarisationsladungen auf der Horizont-Oberfläche
zum elektrischen Feld (6.67)
, also der Faktor
.
6.6 Die Kraftdichte im Clausius-Mosotti-Fall
ist die Spezialisierung von (6.55) auf ebendiesen. Mit (6.10) und (6.58) finden wir
. Mit (6.10) und (6.58) finden wir
.
Kapitel 7
Historische “Kraft-Ausdrücke”
7.1 Die Kelvin-Kraft
Kelvin leitete 1845 [Kel45] den, soweit in der heutigen Literatur bekannt, vermutlich ersten
Ausdruck für eine ponderomotorische Kraft her. Er ist in der Gestalt
vielzitiert und als “Kelvin-Kraft” auch gemeinhin nach ihm benannt.
7.2 Die Helmholtz-Kraft
7.2.1 Klassische Herleitung (gemäß der Becker’schen Überarbeitung)
Traditionell fußt die Herleitung der sogenannten Helmholtz-Kraft auf der Identifizierung der
Energieänderung eines deplazierten Fluidelementi mit der mechanischen Verschiebe-Energie “Kraft
. Verschiebeweg”.
 : : | als Präfix vor einer [auch indirekten] Funktioni vom Ort, bedeutet deren
durch die Deplazierung verursachte Änderung |
| V : | Größe des deplazierten Voluminis |
 V : V : | Oberfläche ( i.e. Rand i.e. Rand ) von V ) von V |
d : : | Oberflächen-Element von  V V |
| U : | innere Energie des Voluminis |
 si : si : | Verschiebeweg |
| fi : | Kraftdichte |
| V tot : | Volumen des gesamten felderfüllten Raums |
| Ei : | elektrisches Feld |
 : : | Potential des elektrischen Feldes |
| Di : | sog. dielektrische Verschiebung |
 : : | Dielektrizitätsfaktor |
 : : | Dichte der elektrischen Ladung |
| n : | Teilchen-Dichte |
| : |
| : |
| : |
| : |
| : |
.
Mit
schreibt man die Änderung der Energiedichte
.
Nun kann mit dem Gaußschen Integral-Satz:
der erste Term von (7.5b) zu Null diskutiert werden, da 
 D fern der Quellen mit der dritten
Potenz des Abstands abfällt, während die Oberfläche
D fern der Quellen mit der dritten
Potenz des Abstands abfällt, während die Oberfläche  V nur quadratisch wächst.
V nur quadratisch wächst.
Die Änderung der Feld-Energie hat damit die Form
.
Die einem Volumini dv verlorengehende Ladungsmenge 
 entschwindet durch die Oberfläche d
entschwindet durch die Oberfläche d :
:
. Das Umschreiben auf die letztere Form (7.8b) erlaubte der Gaußsche Satz. Man ersieht hieraus
leicht2
die Kontinu¨itätsgleichung für die Ladungsdichte in der Form
Völlig analog erhält man eine Kontinu¨itätsgleichung für die Anzahldichte:
, aus der wir auf die Änderung der dielektrischen Suszeptibilität schließen:
.
Mit den beiden Kontinu¨itätsergebnissen schreibt man für die Änderung der inneren Energie vorerst
.
Wendet man auf die Integranden die Produktregel
und auf die ersten Terminos der rechten Seite den Gaußschen Integral-Satz an, dann
erhält man, da die “Oberfläche”  V tot des gesamten felderfüllten Raums V tot sicher
außerhalb der Träger von (Ladungs- und Materie-)Dichte liegt, die Oberflächen-Integrale
, mithin also die ersten Termini der rechten Seite, verschwinden, letztlich . Durch Vergleich mit (7.2) identifiziert man nunmehr unschwer als die Kraftdichte.
V tot des gesamten felderfüllten Raums V tot sicher
außerhalb der Träger von (Ladungs- und Materie-)Dichte liegt, die Oberflächen-Integrale
, mithin also die ersten Termini der rechten Seite, verschwinden, letztlich . Durch Vergleich mit (7.2) identifiziert man nunmehr unschwer als die Kraftdichte.
Bei Belieben kann man nun noch den letzten Terminum unter Zuhilfenahme von
umformen in
.
7.2.2 Nicht ganz so klassische Herleitung (á la Landau)
Die Kraft F auf ein Volumen V kann man in verschiedenen Formen schreiben:
Wegen der Willkür bezüglich der Wahl des Integrationsgebiets ist diese Betrachtung lokal
und wir können auf die Gleichheit der Integranden von (7.19a) und (7.19c) schließen:
.
Landau zerteilt nun sein Volumen so, daß die Oberflächen O auf den Äquipotentialflächen liegen.
Man kann solch ein Volumenelement nun bezüglich des Feldes komplett von der Außenwelt
abschneiden, indem man es sein elektrisches Feld selbst erzeugen läßt durch Ablegen der passenden
Ladungsdichte3
 0E auf den Oberflächen O. Landau gelangt nun zu einem Ausdruck für den Spannungstensorem,
indem er das Volumenelement unter drei Bedingungen dehnt:
0E auf den Oberflächen O. Landau gelangt nun zu einem Ausdruck für den Spannungstensorem,
indem er das Volumenelement unter drei Bedingungen dehnt:
- die Äquipotentialflächen sollen mit den Oberflächen O mitwandern, d.h. die elektrische
Spannung zwischen (Ober- und Unter-)seite soll konstant bleiben:
- es soll kein Materiefluß stattfinden:
- die Temperatur bleibe konstant:
. Diese drei Bedingungen lassen sich nun aber nicht für ein abgeschlossenes System gewährleisten.
Vielmehr müssen, um Bedingung (7.21) zu garantieren, die “Kondensator-”Oberflächen an ein
Ladungsbad, i.e. eine Spannungsquelle angeschlossen werden, und für Bedingung (7.23) ist
analog ein Ankoppeln an ein Wärmebad erforderlich. Landau definiert nun die frei-freie
Energiedichte4
, die die beiden Flüsse berücksichtigt.
Die mechanische Arbeit, die man beim Ziehen an der Oberfläche zu verrichten hat, entspricht dann
der Änderung der frei-freien Energie des Volumenelementi
. Hierbei fällt der erste Term weg, da die Oberfläche nicht verändert werden soll.
Die Forderung nach konstanter Temperatur,  T = 0, fällt nicht mit höheren Weihen vom Himmel;
sie ist schlichtweg die Kapitulation des Physikers vor der Komplexität, die er sich einhandelte,
berücksichtigte er die Temperaturabhängigkeit aller Materialeigenschaften. Man sieht, das Opfer des
ersten Termini von (7.24) an den Gott aller Thermostate trägt die Frucht der ersten Vereinfachung
und wir ernten
T = 0, fällt nicht mit höheren Weihen vom Himmel;
sie ist schlichtweg die Kapitulation des Physikers vor der Komplexität, die er sich einhandelte,
berücksichtigte er die Temperaturabhängigkeit aller Materialeigenschaften. Man sieht, das Opfer des
ersten Termini von (7.24) an den Gott aller Thermostate trägt die Frucht der ersten Vereinfachung
und wir ernten
.
Die Gestalt von Gleichung (7.25a) empfiehlt uns das Programm, das wir auf dem Weg zu einem
Ausdruck für den Spannungstensorem  ij abzuarbeiten haben werden -- Ausklammern von Oi
ij abzuarbeiten haben werden -- Ausklammern von Oi hj
auf deren rechter Seite.
hj
auf deren rechter Seite.
Als hierfür ganz ungemein hilfreich werden sich die beiden Folgerungen
und
erweisen.
Setzen wir nun (7.27) und (7.28) in (7.25) ein,
, dann können wir Oi( h)j allseits wegkürzen, so daß zunächst bleibt.
h)j allseits wegkürzen, so daß zunächst bleibt.
Die ersten beiden Termini von (7.30) bilden zusammen einen Druckterminum, den wir
nun genauer bestimmen wollen. Um ihn greifbarer zu machen, teilen wir ihn in den rein
thermodynamischen Anteil und den auf den Einfluß des Feldes zurückzuführenden Anteil
auf.
Zunächst bemerken wir, daß
, wobei F0 den sonst einfach als Dichte der freien Energie bezeichneten rein thermodynamischen
Anteil der Dichte der frei-freien Energie bezeichnet.
Hätten wir
in Koordinaten des spezifischen Voluminis [, das ja gerade n-1 ist,] geschrieben, fänden wir es
sicher trivial -- so sieht es halt etwas kryptischer aus.
7.2.2.1 Der Spannungstensor
Setzen wir jetzt (7.31) und (7.32) in (7.30) ein, erhalten wir schließlich den Spannungstensorem
.
7.2.2.2 Die Kraftdichte
des elektromagnetischen auf das mechanische Subsystem ist seit (4.13) die Divergenz des
Spannungstensoris:
. Ohne freie Ladungen und ohne Induktionem wird hieraus schließlich die bereits bekannte Helmholtz-Kraftdichte
.
Kapitel 8
Identität von Kelvin-Kraft und Helmholtz-Kraft für Clausius-Mosotti-Fluida
| fs : | Clausius-Mosotti-Symmetriefaktor ( im SO(3)-Falle ist z.B. fs =
1/3 im SO(3)-Falle ist z.B. fs =
1/3 ) ) |
| n : | Dipoldichte |
 : : | molekulare Polarisierbarkeit |
 : : | dielektrischer Suszeptibilitätsfaktor |
| : |
| : |
| : |
| : |
Satz 8.1 Sei
die Kelvin-Kraftdichte1
und die Helmholtz-Kraftdichte auf ein verallgemeinertes Clausius-Mosotti-Fluidum mit einem Feld
am Orte eines einzelnen Multipols, dann sind (Helmholtz und Kelvin)-Kraftdichte identisch.
Beweis:
Die Kelvin-Kraftdichte:
Die Helmholtz-Kraftdichte:
_
Kapitel 9
Swinging Landau
But in our enthusiasm, we could not resist a
radical overhaul of the system, in which all of its
major weaknesses have been exposed, analyzed,
and replaced with new weaknesses.
-
Bruce Leverett:
“Register Allocation in Optimizing Compilers”
| T : | Temperatur |
| s : | Entropiedichte |
| p : | Druck |
| n : | Multipol-Dichte |
| F : | Dichte der freien Energie mit elektromagnetischem Feld |
| F0 : | Dichte der freien Energie ohne elektromagnetisches Feld |
 ij : ij : | Spannungstensor mit elektromagnetischem Feld |
| Wq : | Energie der auf den “Kondensatorplatten” des
Volumenelementi befindlichen Ladungen |
| fcm : | Faktor, um den das lokale Feld am Orte eines Multipols gegenüber dem
makroskopischen E-Feld größer ist |
| Wosc0 : | Oszillations-Energie, die ein Multipol im makroskopischen E-Feld hätte,
i.e. ohne den Faktorem fcm |
| O : | Oberfläche des Landau’schen Volumenelementi |
| h : | Höhe des Landau’schen Volumenelementi |
| U : | elektrische Spannung zwischen den “Kondensatorplatten” |
| : |
| : |
| : |
| : |
9.1 Innere Energie
| v : | spezifisches Volumen |
| : |
| : |
| : |
| : |
| : |
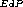 ist die in der Aufspreizung der
Dipole gespeicherte potentielle Energie, was man sich am Modell des aufgeladen werdenden
Kondensatoris klarmachen kann.
ist die in der Aufspreizung der
Dipole gespeicherte potentielle Energie, was man sich am Modell des aufgeladen werdenden
Kondensatoris klarmachen kann.
In einen zeitlichen Verlauf eingebettete Änderungen der Dichte der inneren Energie beschreibt man
am besten, indem man du formal durch dt dividiert ( außerdem wurde noch die Variable v durch
n ersetzt
außerdem wurde noch die Variable v durch
n ersetzt ):
):
Dieser bis hierher recht na¨ive Ansatz läßt zwei Punkte völlig unklar:
- wie geht ein eventuell durch das elektrische Feld hervorgerufene Striktionsdruck in die
Betrachtungen ein ?
- wo bleibt die in den Dipolen gespeicherte kinetische Energie ?
Um zu überprüfen, ob wir nicht im Begriffe sind, die Voraussetzungen von (9.1) überzustrapazieren,
wollen wir (9.2) vergleichen mit einem Ausdruck (9.21), den wir aus einer Modellierung der Dipole
als Dipol-Oszillatores gewinnen.
Um später in Sektioni 9.2 bequemer hantieren zu können, studieren wir zunächst - in bester
buttom-up-Manier - einen einzelnen Dipol-Oszillatorem und danach ein ganzes Ensemble
solcher.
9.1.1 Der getriebene Dipol-Oszillator
Eine linear-elastisch gebundene Ladung q der Masse m in einem elektrischen
Feld1
, die sich zu Zeitpunkt t am Ort r befindet2,
gehorcht der Bewegungsgleichung , die3
durch gelöst wird.
Unser Dipol hat das Moment
, die Polarisierbarkeit
, die kinetische Energie
, die potentielle Energie
, die Oszillations-Energie
und die Oszillations-Leistung
.
9.1.2 Ein Ensemble getriebener Multipol-Oszillatorum im Clausius-Mosotti-Fall
Nachdem das Feld, das ein einzelner Multipol in Umgebung seiner Kollegen verspürt, das um den
Clausius-Mosotti-Faktorem fcm vergrößerte elektrische Feld Ecm = fcmE ist, mag man zunächst
na¨iv versucht sein, die Dichte des elektromechanischen Anteils der inneren Energie des gesamten
Ensembles aller Multipole
zu schreiben -- in offensichtlichem Widerspruch zum [statisch] in keinerlei Hinsicht falsifizierten
Ausdruck
, in dem der Faktor 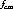 nur in einfacher Potenz auftritt.
nur in einfacher Potenz auftritt.
Nun besteht die Na¨ivität des Ansatzes (9.12) darin, das um den Faktorem fcm gegenüber dem
makroskopischen E vergrößerte lokale Feld, quasi wie a priori existent zu behandeln, während der
über fcm = 1 hinausgehende Feldanteil tatsächlich doch erst durch die Nähe der Kollegen verursacht
wird.
Ein zutreffendes Präparieren des gesamten Ensembles muß deshalb so aussehen:
- Einstellen der thermodynamischen Parameter [T, n], wobei man die einzelnen Multipole
zunächst daran hindert, miteinander und mit dem elektrischen Feld zu interagieren,
indem man ihre Polarisierbarkeit [quasi mit der Schraubzwinge] bei
 = 0 hält
= 0 hält
- Einschalten des elektrischen Feldes. Wegen
 = 0 hat man dabei nur die Vakuum-
Feldenergie zu investieren
= 0 hat man dabei nur die Vakuum-
Feldenergie zu investieren
- meine n
 die Dichte der schon am Polarisations-Spiel teilnehmenden Multipole,
dann beginnt man nun, von n
die Dichte der schon am Polarisations-Spiel teilnehmenden Multipole,
dann beginnt man nun, von n = 0 ausgehend, sozusagen eine Schraubzwinge
nach der anderen zu öffnen. Dabei arbeiten die ihrem Gleichgewicht im E-Feld
entgegenstrebenden Multipole an der Schraubzwinge. Gleichzeitig erhöhen sie für all
ihre Kollegen das lokale Feld um einen kleinen Anteil
= 0 ausgehend, sozusagen eine Schraubzwinge
nach der anderen zu öffnen. Dabei arbeiten die ihrem Gleichgewicht im E-Feld
entgegenstrebenden Multipole an der Schraubzwinge. Gleichzeitig erhöhen sie für all
ihre Kollegen das lokale Feld um einen kleinen Anteil
.
9.1.2.1 Energiebilanz beim Öffnen einer einzigen Schraubzwinge
Vereinbaren wir das Energieniveau eines einzelnen Dipols, den wir durch Setzen von  = 0 in dem
Zustand eingefroren haben, den er auch in feldfreier Umgebung hätte, zu Null, dann wurde im Feld
beim Öffnen der
= 0 in dem
Zustand eingefroren haben, den er auch in feldfreier Umgebung hätte, zu Null, dann wurde im Feld
beim Öffnen der  -Schraubzwinge bei einem Dipolmomento p die Energie pjEcmj frei. Diese
wurde [im Falle des linearen Oszillatoris] zur Hälfte in die elastische Bindung investiert
-Schraubzwinge bei einem Dipolmomento p die Energie pjEcmj frei. Diese
wurde [im Falle des linearen Oszillatoris] zur Hälfte in die elastische Bindung investiert
und zur anderen Hälfte an der Schraubzwinge abgearbeitet.
9.1.2.2 Energiebilanz beim Öffnen aller Schraubzwingen
Das Feld am Ort des Multipols ist natürlich eine Funktion der Dichte n der schon “freigelassenen”
Multipole, so daß wir mit Aufintegrieren aller Beiträge von der ersten bis zur letzten Schraubzwinge
der schon “freigelassenen”
Multipole, so daß wir mit Aufintegrieren aller Beiträge von der ersten bis zur letzten Schraubzwinge
erhalten.
Mit
ist das Integral selbst nun
.
Die Dichte der potentiellen Energie eines Ensembles von Multipolen ist nach dieser Betrachtung also
in der Tat
-- angesichts (9.13c) sehr zu unserer Beruhigung.
Mithin ist die Dichte des gesamten elektrischen Anteils der inneren Energie des ganzen Ensembles
oszillierender Multipole also
.
9.2 Landau revisited
| Q : | Ladung auf der Oberfläche |
| : |
| : |
| : |
| : |
Der thermodynamische Anteil der Dichte der freien Energie ist wie gewohnt
, nun aber, im Unterschied zu Landau, mit elektrischem Feld. Dies ist bezüglich des Ladungsaustausches keine freie Energie. Die Arbeit am
Ladungsbad wird in der folgenden Betrachtung explizit berücksichtigt.
Die mechanische Leistung, die wir an unserem Volumenelemento erbringen, ist
, also
. Term (9.23d) ist gerade das Negativum der Leistung am “Kondensatori” [i.e. den Oberflächen-
Ladungen] des Volumenelementi, oder andersherum betrachtet, die Leistung der Oberflächen-
Ladungen am “Ladungsbad”, an das man das Kondensatorelement anschließen muß,
um die Vorgabe  zu gewährleisten. Diese Leistung haben wir zwar
mechanisch erbracht, sie kam jedoch nicht unserem Dielektriko zugute, sondern eben dem
Ladungsbad.
zu gewährleisten. Diese Leistung haben wir zwar
mechanisch erbracht, sie kam jedoch nicht unserem Dielektriko zugute, sondern eben dem
Ladungsbad.
Das Programm, das nun ansteht, um einen Ausdruck für den Spannungstensorem  ij zu finden, ist,
auf der rechten Seite von (9.23) Oi
ij zu finden, ist,
auf der rechten Seite von (9.23) Oi auszuklammern.
auszuklammern.
Zu diesem Behufe kommen uns die beiden
Beziehungen5
wie gerufen6,
deren erstere Konsequenz der Forderung (7.21), und deren letztere Konsequenz der Forderung (7.22)
ist.
9.2.1 Termini (9.23a.1)+(9.23c.1)
Ersetzt man zunächst in (9.23c.1)  gemäß (9.24b),
gemäß (9.24b),
, und bemerkt, daß ohne elektromagnetisches Feld ist, dann liefern die Termini (9.23a.1)+(9.23c.1) zusammen gerade
.
9.2.2 Termini (9.23a.2)+(9.23a.3)
präsentieren sich schon in der gewünschten Form.
9.2.3 Term (9.23b.1)
fällt trivialerweise weg, da natürlich die Dichte des feldfreien Anteils der frei-freien Energie nicht
vom Feld abhängt.
9.2.4 Termini (9.23b.2)+(9.23c.2)
spaltet man nach der Produktregel auf in . Dessen erster Term fällt ohne weiteres weg, da fcm nicht vom Feld E abhängig
ist7,
und aus dem zweiten wird, wenn wir (9.24b) applizieren . Den dritten Terminum schließlich gewinnt man durch direktes Einsetzen von (9.11)
.
9.2.5 Term (9.23b.3)
Die Ableitung nach E in
führt man einfach aus und setzt (9.24a) ein, so daß man findet .
9.2.6 Term (9.23c.3)
ist trivialerweise Null.
9.2.7 Term (9.23d)
Die Leistung, die wir am Ladungsbad erbringen, ist
.
9.2.8 Der Spannungstensor
Jetzt, da in allen Terminis O ausfaktoriert wurde, können wir die Co-Faktores zum
Spannungstensori aufsummieren:
ausfaktoriert wurde, können wir die Co-Faktores zum
Spannungstensori aufsummieren:
, q.e. in summa
. Die erste Teilsumme (9.36a) entspricht just dem statischen Ausdruck, während mit (9.36b) ein
Ausdruck hinzukommt, der auf die Berücksichtigung der kinetischen Energie der Multipol-
Oszillatorum zurückzuführen ist. Man kann ihn zur genaueren Analyse evtl. noch detaillierter
schreiben. Er ist in der Tat rein kinetischen Ursprungs, denn wie man sieht, verschwindet er für

 0.
0.
9.2.9 Die Kraftdichte
ist mit (9.36) und (9.37c) nun schließlich
.
Kapitel 10
Epilog
Bisher haben rein mikroskopische Ansätze zur Bestimmung ponderomotorischer Kräfte neben rein
makroskopischen ein Dasein gegenseitiger Nicht-Kenntnis geführt.
10.1 Das Lager der Mikroskopiker
Protagonisten des mikroskopischen Lagers sind Penfield und Haus sowie de Groot und Suttorp,
deren Darstellungen auch heute nur wenig hinzuzufügen ist.
Bezeichnend für mikroskopische Herleitungen sind Kraft-Ausdrücke in Gestalt der Kelvin-
Kraft.
10.2 Das Lager der Makroskopiker
Protagonisten des makroskopischen Lagers sind Helmholtz und Landau. Auch ihren Darstellungen
ist heute, knapp ein Achtel Jahrtausend nach Helmholtz’ Veröffentlichung nur Marginales
hinzuzufügen. Bedauerlicherweise hat das rekursive Abschreiben der Helmholtz’schen Arbeit nur in
der Darstellung zu geringfügigen Verbesserungen geführt [und auch da nur bei Panofsky & Phillips
und Becker & Sauter], in der Tiefe das Verständnisses sind im Verlaufe dieser Historie
Verluste zu beklagen. Einziges Lob gebührt Landau, der mit seinem eigenen Ansatz
das inhärente Lokalitäts-Manko der Helmholtz’schen Herleitung aus der Welt schaffen
konnte.
Typisch für makroskopische Herleitungen sind Ausdrücke, deren Gestalt dem Helmholtz’schen
ähnelt.
Die Dispute im wissenschaftlichen Lager um den richtigen Ausdruck für die Kraft sind Legende.
Hier konnte gezeigt werden, daß beide Darstellungen der ponderomotorischen Kraft für
verallgemeinerte Clausius-Mosotti-Fluida in der Tat nur verschiedene Formulierungen ein und
derselben Kraft sind. Und mit Recht hätte man am Vermögen der Physiker gezweifelt, wäre etwas
anderes zu Tage getreten.
10.3 Eine Brücke
Sehen wir uns noch einmal rückblickend an, wie der Bau dieser Brücke von beiden Lagern
ausgehend erfolgte:
- einerseits wurde das Landau-Modell
- zeitabhängig verallgemeinert und
- auf das verallgemeinerte Clausius-Mosotti-Fluid spezialisiert
- andererseits wurde das de Groot-Modell
- auf alle Multipol-Ordnungen erweitert und
- auf das verallgemeinerte Clausius-Mosotti-Fluid spezialisiert
.
Dies brachte folgende Ergebnisse zutage:
.
10.4 Eine Krücke
wird in gewisser Hinsicht wohl bleiben müssen die hier demonstrierte Variante des Fremdwort-
Gebrauchs.
Führen wir uns einige diskutable Möglichkeiten des Gebrauchs von Fremdworten vor
Augen:
- man beläßt Fremdworte gänzlich originär, d.h. man konjugiert und dekliniert sie gemäß den
Regeln ihrer Ursprungssprache. Dies setzt beim Autori weitgehende Sprachperformanz
all der Ursprungssprachen voraus, aus denen er Fremdworte rekrutiert1.
Vom Leser wird die entsprechende Sprachkompetenz oder wenigstens Lernbereitschaft
vorausgesetzt.
- man ergreift muttersprachlichen Besitz von Fremdworten[, macht sie also zu
Lehnworten,] und konjugiert und dekliniert sie nach den Regeln der eigenen Sprache.
Diese Variante wird von Nationibus wie Frankreich oder der Türkei praktiziert. Sowohl
vom Leser wie auch vom Autori werden nur die muttersprachlichen Fertigkeiten
erwartet. Es wird aber nur von [gebildeten] Menschen, die sowohl der jeweiligen
Ursprungssprache als auch der Muttersprache mächtig sind, zu erwarten sein, daß sie
ein Regelwerk ersinnen und praktizieren, nach dem Fremdworte zu importieren sind.
Frankreich hält sich hierzu im Rahmen der Academie Francaise einen Stab von
Sprachexperten, die diesen Dienst erbringen. Dies korrespondiert mit dem allgemein
eher zentralistischen Habitui Frankreichs.
- rekrutiert man Fremdworte nur aus einer Ursprungssprache, bliebe die Möglichkeit,
sich gänzlich der Ursprungssprache zu bedienen. Dies war noch bis ins 19. Jahrhundert
hinein üblich, führte aber zu einer Art Herrschaftssprache mit der Folge der
Ausgrenzung der nicht-dieser-Sprache-Kundigen. Dies ist wohl die aristokratischste der
hier diskutierten Varianten.
- man benutzt Fremdworte gemäß der momentanen deutschen Praxis und dekliniert nur
den Numerum. Das dürfte die volxnächste dieser Varianten sein. Es ist aber auch die
inkonsequenteste.
Anhang A
Linguistische Ergänzung
A.1 Arithmetischer Ausdruck
Im Zusammenhang mit arithmetischen Ausdrücken wurden die Namen verschiedener
Nicht-Terminale verwendet, deren syntaktische Rollen im Rahmen folgenden
Produktionensystems1
präzisiert seien:
| Ausdruck ::= | [“-”] Term { (“+”|“-”) Term }; |
| Term ::= | Faktor { [“/”] Faktor }; |
| Faktor ::= | Ausdruck | Zahl; |
| Zahl ::= | Variable | Konstante; |
| Variable ::= | Tensorkomponente | Funktionswert; |
| Konstante ::= | Ganzzahl | Dezimalbruch | Gleitkommazahl; |
| Tensorkomponente ::= | ...; |
| Funktionswert ::= | ...; |
| Ganzzahl ::= | ...; |
| Dezimalbruch ::= | ...; |
| Gleitkommazahl ::= | ...; |
Anhang B
Mathematische Ergänzungen
B.1 Beweis zu Satz 6.1
Wir können den Satz um den Preis, den Indicem für die Nummer der Ladung innerhalb eines
Atoms mitnotieren zu müssen, sogar noch schärfer, nämlich für jede einzelne Ladung, formulieren:
Den Beweis führen wir mittels vollständiger Induktionis:
B.1.1 n = 0
Für n = 0 wird offensichtlich, mit  , der Definitioni für elektrische Monopole
, der Definitioni für elektrische Monopole
 (
( (5.12a)
(5.12a) ), der Ladungserhaltung
), der Ladungserhaltung  , der nullten Ableitung
, der nullten Ableitung
 und der Nicht-Existenz magnetischer Monopole
und der Nicht-Existenz magnetischer Monopole 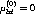 (
( (5.13a)
(5.13a) ),
),
identisch zu 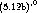 .
.
B.1.2 n n + 1
n + 1
Angenommen, der Satz gelte für n,
, dann überzeugen wir uns nun davon, daß er auch für n + 1 gilt.
Dazu multiplizieren wir zunächst beiderseits mit rbdh h
h
B.1.2.1 Drei kleine Helferlein
Um den weiteren Lösungsweg zu zergliedern, behelfen wir uns dreier Lemmata
- Lemma
Beweis
Hier kommt nichts weiter zum Zuge als die Normierung der r-Dyade gemäß Definitioni (5.12)
_
- Lemma
Beweis
_
- Lemma
Beweis
__
Wir substitu¨ieren nun in den einzelnen Terminis von (B.4) die entsprechenden Faktores durch die
rechten Seiten unserer Lemmata:
.
B.1.2.2 Garbage Annihilation
Nun trachten wir noch danach, uns der Richtigkeit der Behauptung
zu vergewissern.
Hierzu bemühen wir die alte a × (b × c) = (b(ac) - c(ab))-Identität, die [etwas umgestellt] in
Komponenten
, in unserem speziellen Fall also lautet. Mit ihr wird der letzte Term von (B.11) zu , dessen erster Term mit Blick auf (5.12d) nun unschwer mit der linken Seite von (B.11) zu
identifizieren ist, während dessen zweiter -- wie könnte es anders sein -- sich mit dem ersten
Termino von (B.11) annulliert.
B.1.2.3 Finale
Subtrahieren wir nun (B.11) von (B.10), dividieren durch den omnipräsenten Faktorem n+2 und
wenden die Produktionem (n)h ::= (n+1) an, dann zeigt sich unsere Gleichung in der Form
; nichts anderes als (B.3) mit (n) ::= (n+1)
_
Anhang C
Lie-Gruppen und Lie-Algebren in der Physik
An verschiedenen Stellen trifft man in der physikalischen Theorie Strukturen mit total-
antimetrischem Produkt an, z.B. den Vertauschungsrelationibus der Quantenmechanik oder den
Poisson-Klammern der klassischen Mechanik.
Wir werden in diesem Abschnitt sehen, daß dies kein Zufall ist und uns ein solches Produkt quasi
zwangsläufig begegnen muß.
C.1 Symmetrien
Üblicherweise betten wir Physiker unsere Modelle in ein einmal gewähltes [oft kartesisches]
Koordinatensystem in der Raum-Zeit ein. Da die Natur sich aber keineswegs danach richtet, wie uns
belieben, unser Koordinatensystem zu legen, besitzt unser Koordinatensystem Freiheiten, die die
Natur nicht auszuschöpfen gedenkt. Mit anderen Worten: weil der Beschreibungsvorrat unseres
Modells über die Bewegungsmöglichkeiten der Natur hinausgeht, sehen wir in unserem Modell
Symmetrien relativ zur Natur.
- Zunächst haben wir (was die
Raum-Zeit betrifft) in einem isotropen Raum mit konstanter Lichtgeschwindigkeit die
Wahl eines Skalierungsfaktoris frei. Die Konsequenzen freier Skalierungsfaktorum auf
eine physikalische Theorie zu untersuchen, ist Domäne der Dimensionsanalyse (siehe
z.B. [Gör75]).
- Weiterhin können wir unser Koordinatensystem in jeder der vier Raumrichtungen
verschieben (transferieren), ohne daß die Qualität unseres Modells, die Natur zu
beschreiben, sich ändert.
- Wir können das Koordinatensystem in allen drei Richtungen um die Zeit-Achse drehen.
- Wir können das Koordinatensystem sich mit konstanter Geschwindigkeit bewegen
lassen.
- Wir können die Zeit-Achse spiegeln.
- Wir können die Orientierung der räumlichen Hyperebene invertieren, d.h. eine oder
drei Raumachsen spiegeln.
Jeder dieser Symmetrien entspricht als Symmetrie-Gruppe jeweils eine bestimmte Untergruppe der
Poincaré-Gruppe.
Die Willkür in der Wahl unseres Koordinatensystems sieht so aus, daß es ganze Klassen äquivalenter
Koordinatensysteme gibt, die jeweils dieselbe Physik beschreiben. Mit der Existenz von Äquivalenzklassen
eindeutig verknüpft ist immer eine Äquivalenzrelation. Diese Äquivalenzrelation ist in unserem Falle
die Invarianz gegen die Operationem von Elementis einer Lie’schen-Transformationsgruppe
nämlich der vollen Poincaré-Gruppe. Das heißt, die Äquivalenzklassen sind die
Orbits1
eines beliebigen Koordinatensystems unter der vollen Poincaré-Gruppe.
Nach dem bisher Gesagten ist klar, daß jede, nach den Voraussetzungen des ersten Abschnitts
konstru¨ierte, physikalische Theorie zwangsläufig die entsprechenden Symmetrien birgt, ob man sie
nun offenlegt oder nicht. Versucht man diese Offenlegung unter direkter Zuhilfenahme
kontinuierlicher Gruppen, dann handelt man sich unmittelbar ein, als adäquate mathematische
Theorie die Analysis auf Mannigfaltigkeiten handhaben zu müssen. Zur großen Vereinfachung hat
die Untersuchung kontinu¨ierlicher [Lie’scher] Gruppen gezeigt, daß man ohne wesentlichen
Informationsverlust, die topologischen Eigenschaften Lie’scher -Gruppen gegen algebra¨ische eintauschen
kann2.
Diese Korrespondenz ist keine 1:1-Korrespondenz. Vielmehr sind Lie-Gruppen eindeutig als direktes
Produkt einer diskreten Gruppe mit einer einfach-zusammenhängenden topologischen Gruppe
darstellbar und es existiert eine 1:1-Korrespondenz zwischen dem mit dem Gruppen-Einheits-
Elemento einfach-zusammenhängenden Teil und der Lie-Algebra. Am Beispiel einer Koordinaten-
Transformationis entlang einer “geraden” Linie ( in dem Sinne, daß man nur einen Parameter t
der Gruppe vari¨iert
in dem Sinne, daß man nur einen Parameter t
der Gruppe vari¨iert ) durch die Transformationsgruppe, ist diese Korrespondenz eine
Exponentialfunktion:
) durch die Transformationsgruppe, ist diese Korrespondenz eine
Exponentialfunktion:
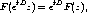
| (C.1) |
wobei D der zum Gruppen-Parameter t gehörige Differentialoperator, etD die Koordinaten-
Transformation und F(z) eine zu transformierende Funktion ist. Ist z.B. t der Parameter einer
linearen Translationis, dann ist D = 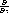 und etDz = t + z, i.e. F(t + z) = etDF(z) - die Taylor-
Entwicklung.
und etDz = t + z, i.e. F(t + z) = etDF(z) - die Taylor-
Entwicklung.
Damit hat man nun die Brücke von den Transformations-[Lie-]Gruppen, die die Symmetrien unserer
physikalischen Modelle beschreiben, zu den Lie-Algebren geschlagen. Der große Gewinn beim
Übergang von den Lie-Gruppen zu den Lie-Algebren besteht darin, daß man sozusagen die
topologischen Eigenschaften der Gruppe gegen die Operationem der Algebra eintauscht, mit der
sich dann viel leichter rechnen läßt.
Literatur
[Bal75] Radu Balescu. Equilibrium and Nonequilibrium Statistical Mechanics. John
Wiley & Sons, New York, 1975.
[Bal88] Radu Balescu. Transport Processes in Plasmas, Band 1. North Holland
Publishing Company, Amsterdam, 1988.
[Bau95] Dieter Bauer. Oszillationszentrums-Dynamik in starken Laserfeldern.
Diplomarbeit, Technische Hochschule Darmstadt, 01 1995.
[BK67] Radu Balecsu und T. Kotera. On the Covariant Formulation of Classical
Relativistic Statistical Mechanics. Physica, 33: 558..580, 1967.
[BKP67] Radu Balecsu, T. Kotera und E. Piña. Lorentz Transformations in Phase Space
and in Physical Space. Physica, 33: 580..594, 1967.
[Bor81] Max Born. Optik. Springer-Verlag, Berlin, 3. Auflage, 1981. Reprint:
photomechanischer Nachdruck der Original-Ausgabe von 1932.
[Bou65] John Bourke. Englischer Humor. Number 212 in Kleine Vandenhoeck-Reihe.
Vandenhoek & Ruprecht, Göttingen, Germany, 1965.
[BS63] Richard Becker und Fritz Sauter. Theorie der Elektrizität, Band 2.
B. G. Teubner, Stuttgart, Germany, 9. Auflage, 1963.
[BS69a] Richard Becker und Fritz Sauter. Theorie der Elektrizität, Band 1.
B. G. Teubner, Stuttgart, Germany, 19. Auflage, 1969.
[BS69b] Richard Becker und Fritz Sauter. Theorie der Elektrizität, Band 3.
B. G. Teubner, Stuttgart, Germany, 1. Auflage, 1969.
[BW86] Radu Balecsu und Boris Weyssow. A Manifestly Gauge-Invariant Hamiltonian
Theory of the Oscillation-Centre Dynamics. Journal of Plasma Physics, 37(3):
449..471, 1986.
[BW87] Radu Balecsu und Boris Weyssow. A Manifestly Gauge-Invariant Hamiltonian
Theory of the Oscillation-Centre Dynamics. Journal of Plasma Physics, 37(3):
467..486, 1987.
[BW88] Radu Balecsu und B. Weyssow. Hamiltonian Theory of the Generalized
Oscillation-Centre Transformation. Journal of Plasma Physics, 39(1): 81..102,
1988.
[Che76] F.F. Chen. Introduction to Plasma Physics. Plenum Press, New York, 1976.
[CJS63] Douglas G. Currie, T.F. Jordan und E.C.G. Sudarshan. Relativistic
Invariance and Hamiltonian Theories of Interacting Particles. Reviews of Modern
Physics, 35(2): 350..375, April 1963.
[Cro88] B.J.B. Crowley. Derivation of the Stress-Tensor for High-Frequency Radiation
in Isotropic Dispersive Matter by Generalisation of the Helmholtz Method. Atomic
Weapons Establishment Report O 22/88, UK Ministry of Defence, 1988.
[Cur63] Douglas G. Currie. Interaction contra Classical Relativistic Hamiltonian
Particle Mechanics. Journal of Mathematical Physics, 4(12): 1470..1488, December
1963.
[Dir49] Paul Adrien Maurice Dirac. Forms of Relativistic Dynamics. Reviews of
Modern Physics, 21(3): 392..399, July 1949.
[Dur66] Emile Durand. Électrostatique, Band III de[r|s] Méthodes de Calcul
Diélectriques. Masson et Cie, Paris, 1966.
[FK98] B.U. Felderhof und H.J. Kroh. Hydrodynamics of Magnetic and Dielectric
Fluids in Interactions with the Electromagnetic Field. to be published, November
1998.
[Gör75] Henry Görtler. Dimensionsanalyse. Ingenieurwissenschaftliche Bibliothek.
Springer-Verlag, Berlin . Heidelberg . New York, 1975. ISBN 3-540-06937-2.
[Gro69] Sybren Ruurds de Groot. The Maxwell Equations, Band IV de[r|s] Studies
in Statistical Mechanics. North Holland Publishing Company, Amsterdam, 1969.
ISBN 0-7204-1104-1.
[GS72] Sybren Ruurds de Groot und L.G. Suttorp. Foundations of Electrodynamics.
North Holland Publishing Company, Amsterdam, 1972. ISBN 0-7204-0248-4.
[Hel81] Hermann Ludwig Ferdinand von Helmholtz. Ueber die auf das Innere
magnetisch oder dielectrisch polarisirter Körper wirkenden Kräfte. Annalen der
Physik und Chemie, 13(7): 385..406, 1881.
[Kel45] William Thomson Kelvin. The Cambridge and Dublin Mathematical
Journal..., Cambridge, November 1845.
[Kib66] T.W.B. Kibble. Mutual Refraction of Electrons and Photons. Physical Review,
150(4): 1060..1069, October 1966.
[KJ87] G.W. Kentwell und D.A. Jones. The Time-Dependent Ponderomotive Force.
Physics Reports, 145(6): 319..403, 1987.
[Kru62] Martin Kruskal. Asymptotic Theory of Hamiltonian and other Systems with
all Solutions Nearly Periodic. Journal of Mathematical Physics, 3(4): 806..828,
July/August 1962.
[Ld96a] Richard Lee <dicklee@llnl.gov>.
Laser-Induced Filamentation. UCRL-ID-119170, September 1996. http://www.
llnl.gov/science_on_lasers/10PlasPhys/PPh_FV-11.html.
[Ld96b] Richard Lee <dicklee@llnl.gov>. Laser-Plasma Instabilities. UCRL-ID-119170,
September 1996. http://www.llnl.gov/science_on_lasers/10PlasPhys/PPh-C_
LPInst.html.
[Lit83a] Robert G. Littlejohn. Hamiltonian Formulation of Guiding Centre Motion.
Physics of Fluids, 24(9): 1730..1749, September 1983?
[Lit83b] Robert G. Littlejohn. Variational Principles of Guiding Centre Motion.
Nuclear Fusion, 29(1): 111..125, 1983.
[LL85] Lew Davidowitsch Landau und E.M. Lifschitz. Elektrodynamik der Kontinua,
Band 8 de[r|s] Lehrbuch der Theoretischen Physik. Akademie-Verlag, Berlin,
4. Auflage, 1985.
[Lor80a] H.A. Lorentz. Annalen der Physikalischen Chemie, (9): 641 ff.., 1880.
[Lor80b] L. Lorenz. Annalen der Physikalischen Chemie, (9): 70 ff.., 1880.
[Max73] James Clerk Maxwell. Electricity and Magnetism. Oxford, 1873.
[Mos36] O.F. Mosotti. Sur les forces qui régissent la constitution intime des corps. 1836.
[Mul85] Peter Mulser. Radiation Pressure on Macroscopic Bodies. Journal of the Optical
Society of America B, 2(11): 1814..1829, November 1985.
[Mul89] Peter Mulser. Physical Picture of Parametric Phenomena and Ponderomotive
Effect in Solids. IAP Report 125/89, Technische Hochschule Darmstadt, Institut
für Angewandte Physik, Darmstadt, October 1989.
[PH67] Paul jr. Penfield und Hermann A. Haus. Electrodynamics of Moving Media,
Band 40 de[r|s] Research Monograph. MIT Press, Cambridge, MA, 1967.
[PP55] Wolfgang K. . Panofsky und Melba Phillips. Classical Electricity and
Magnetism. Addison-Wesley Publishing Company, Reading, Massachusetts,
1. Auflage, 1955.
. Panofsky und Melba Phillips. Classical Electricity and
Magnetism. Addison-Wesley Publishing Company, Reading, Massachusetts,
1. Auflage, 1955.
[Ste70a] David P. Stern. Direct Canonical Transformations. Journal of Mathematical
Physics, 11(9): 2776..2781, September 1970.
[Ste70b] David P. Stern. Kruskal’s Perturbation Method. Journal of Mathematical
Physics, 11(9): 2771..2775, September 1970.
[Ste71a] David P. Stern. The Canonization of Nice Variables. Journal of Mathematical
Physics, 12(10): 2226..2231, October 1971.
[Ste71b] David P. Stern. Classical Adiabatic Perturbation Theory. Journal of
Mathematical Physics, 12(10): 2231..2242, October 1971.
[Str85] Michael A. Stroscio. Relativistic Derivation of the Ponderomotive Force
Produced by Two Intense Laser Fields. IEEE Transactions on Plasma Science,
PS-13(1): 16..18, February 1985.
[SW89] Crosbie W. Smith und Norton M. Wise. A biographical study of Lord Kelvin.
Cambridge University Press, Cambridge, U.K., 1989.
[Tho45a] William Thomson. Demonstration of a Fundamental Proposition in Electricity.
The Cambridge Mathematical Journal, IV: 223..??, 1845.
[Tho45b] William Thomson. Note on Induced Magnetism in a Plate. The Cambridge and
Dublin Mathematical Journal, i: 34..37, 1845.
[Tho45c] William Thomson. On the Elementary Laws of Statical Electricity. The
Cambridge and Dublin Mathematical Journal, i: 75..96, May 1845.
[Tho46] William Thomson. On a Mechanical Representation of Electric, Magnetic and
Galvanic Forces. The Cambridge and Dublin Mathematical Journal, ii: 61..64,
November 1846.
[Tho47a] William Thomson. On a System of Magnetic Curves. The Cambridge and
Dublin Mathematical Journal, ii: 240, May 1847.
[Tho47b] William Thomson. On Certain Definite Integrals Suggested by Problems in
the Theory of Electricity. The Cambridge and Dublin Mathematical Journal, ii:
109..122, March 1847.
[Tho47c] William Thomson. On the Forces Experienced by Small Spheres under Magnetic
Influence; and on some of the Phenomena Presented by Diamanetic Substances.
The Cambridge and Dublin Mathematical Journal, ii: 230..235, May 1847.
[Tho48a] William Thomson. Geometrical Investigations Regarding Spherical Conductors.
The Cambridge and Dublin Mathematical Journal, iii: 266..274, July 1848.
[Tho48b] William Thomson. Geometrical Investigations with Reference to the Distribution
of Electricity on Spherical Conductors. The Cambridge and Dublin Mathematical
Journal, iii: 141..148, March 1848.
[Tho48c] William Thomson. A Statement of the Principles on which the Mathematical
Theory of Electricity is Founded. The Cambridge and Dublin Mathematical Journal,
iii: 131..140, March 1848.
[Tho49a] William Thomson. Effects of the Electrical Influence on Internal Spherical, and
on Plane Conducting Surfaces. The Cambridge and Dublin Mathematical Journal,
iv: 276..284, October 1849.
[Tho49b] William Thomson. Geometrical Investigations Regarding Spherical Conductors.
The Cambridge and Dublin Mathematical Journal, v: 1..9, September 1849.
[Tho76] Thompson. The Life of Lord Kelvin. Chelsea Publishing Company, New York,
2. Auflage, 1976. 2 volumes.
[Vle32] John Hasbrouk van Vleck. The Theory of Electronic and Magnetic
Susceptibilities. Lowe Brydone Printers Ltd., London, 1932.
[Vle52] John Hasbrouk van Vleck. The Theory of Electronic and Magnetic
Susceptibilities. Oxford University Press, London, 1952. (Nachdruck).
[Wey31] Hermann Weyl. Gruppentheorie und Quantenmechanik. Leipzig, 2. Auflage,
1931.
[Wil87] David B. Wilson. Kelvin and Stokes: a comparative study in Victorian physics.
Adam Hilger@IOP Publishing Ltd., Bristol, England, 1987.
[Wil90] David B. Wilson, Hrsg.. The correspondence between Sir George Gabriel Stokes
and Sir William Thomson, Baron Kelvin of Largs, Band 1, 1846..1869. Cambridge
University Press, Cambridge, U.K., 1990.
[Zim95] Dieter E. Zimmer. Sonst stirbt die deutsche Sprache. DIE ZEIT, 50(26): 42,
06 1995.
[ZS87] Shitong Zhu und Wenda Shen. General Relativistic Ponderomotive Force in
a Moving Medium. Journal of the Optical Society of America B, 4(5): 739..742,
September 1987.
| My pen is at the bottom of a page, |
| Which, being finished, here the story ends; |
| |
| ’Tis to be wished, it had been sooner done, |
| But stories somehow lengthen when begun. |
| |
| - George Gordon, alias Lord Byron |
 <1999/12/01> auf TEX 3.14159 (Web2C version 7.3.1) in einer
kerning-optimierten Variante des Fonts Computer Modern in der Basisgröße 10 Punkt. Die deutschen
Sprachspezifica wurden durch das “german.sty”-Paket 2.5e und die Postscript-Graphiken mit dem “epsfig.sty”-Paket
eingebunden. Als Entwicklungsumgebung diente Xemacs 19.16 mit AucTeX 9.7, wobei Xdvik 20.57 zur
Vorbetrachtung diente. Das gesamte TEX-Paket war eine leicht modifizierte Variante der teTEX-Distributionis für
Linux in der Versioni 1.0.7. Die Rechnerplattform war ein unter Redhat-Linux 5.0, Kernel 2.2.14 laufender
Am486.
<1999/12/01> auf TEX 3.14159 (Web2C version 7.3.1) in einer
kerning-optimierten Variante des Fonts Computer Modern in der Basisgröße 10 Punkt. Die deutschen
Sprachspezifica wurden durch das “german.sty”-Paket 2.5e und die Postscript-Graphiken mit dem “epsfig.sty”-Paket
eingebunden. Als Entwicklungsumgebung diente Xemacs 19.16 mit AucTeX 9.7, wobei Xdvik 20.57 zur
Vorbetrachtung diente. Das gesamte TEX-Paket war eine leicht modifizierte Variante der teTEX-Distributionis für
Linux in der Versioni 1.0.7. Die Rechnerplattform war ein unter Redhat-Linux 5.0, Kernel 2.2.14 laufender
Am486.


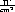 relevant. Diese Intensität
relevant. Diese Intensität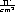 gehört für viele Forschergruppen schon zum Alltag.
Insbesondere die Erkenntnis, daß ponderomotorische Kräfte
gehört für viele Forschergruppen schon zum Alltag.
Insbesondere die Erkenntnis, daß ponderomotorische Kräfte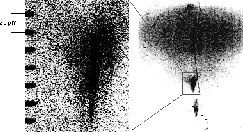

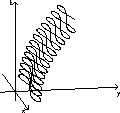
 gerade Strecke bzw. Sichel
gerade Strecke bzw. Sichel ) - ohne daß sich am Phänomen der säkularen
Beschleunigung
) - ohne daß sich am Phänomen der säkularen
Beschleunigung

 )
) 





 die
partielle Ableitung nach der Zeit
die
partielle Ableitung nach der Zeit die totale. Wird eine Größe
die totale. Wird eine Größe 
 .
.






 (
( ), ist über alle
möglichen Permutation
), ist über alle
möglichen Permutation
 letztere bei zusätzlich
eingeschaltetem “statischen” B-Feld
letztere bei zusätzlich
eingeschaltetem “statischen” B-Feld ).
).


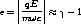
 z.B. in Reduce
z.B. in Reduce )
implementierbar ist
)
implementierbar ist siehe die folgende Beschreibung des Bauer
siehe die folgende Beschreibung des Bauer )
zurückbleibt, ist doch zu bemerken, daß das Vorgehen an sich aus erkenntnistheor
)
zurückbleibt, ist doch zu bemerken, daß das Vorgehen an sich aus erkenntnistheor
 von etwa 0
von etwa 0 dem Ladungsbad
dem Ladungsbad ) geleistete Arbeit
) geleistete Arbeit  W
W 



 Atom
Atom ) aus und liefert über eine Taylor-Entwicklung
) aus und liefert über eine Taylor-Entwicklung sobald die
Nichtlinear
sobald die
Nichtlinear ), d.h. die unserer Detektorträgheit
), d.h. die unserer Detektorträgheit
 siehe z.B. Chen, Kap. 8, Gl. (8.39),
siehe z.B. Chen, Kap. 8, Gl. (8.39),  ) hinaus.
) hinaus.
 solange
Ionisation
solange
Ionisation ) besteht die Target
) besteht die Target Atom
Atom ). Die Bindung einer
Ladung
). Die Bindung einer
Ladung





 siehe z.B.
siehe z.B.  ).
).












 Dichte der extensiven Größe
Dichte der extensiven Größe ) über das interessante
Raumgebiet. Der Vorgang der Integrationis über ein Raumgebiet wird in der Mathematik greifbar
gemacht, indem man - im Grenzwert betrachtet - das Integrationsgebiet in immer kleinere
Volumenelementa zerlegt, deren Beitrag man aufsummiert.
) über das interessante
Raumgebiet. Der Vorgang der Integrationis über ein Raumgebiet wird in der Mathematik greifbar
gemacht, indem man - im Grenzwert betrachtet - das Integrationsgebiet in immer kleinere
Volumenelementa zerlegt, deren Beitrag man aufsummiert.

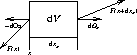




 Granul
Granul ).
).
 meistens
wird dies die Summe der Lorentz-Kräfte
meistens
wird dies die Summe der Lorentz-Kräfte )
)

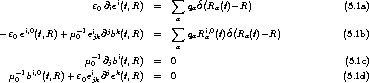
 e.s. in
praxi Atome, Moleküle, Kristalle
e.s. in
praxi Atome, Moleküle, Kristalle ), dann kann man die Maxwell-Gleichungen umschreiben, indem
man
), dann kann man die Maxwell-Gleichungen umschreiben, indem
man
 Schwerpunkt von Ladung, Masse,
Schwerpunkt von Ladung, Masse,  ) mit dem Parameter
) mit dem Parameter 



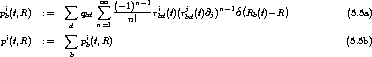




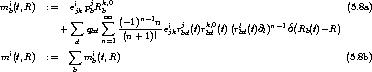
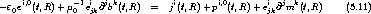







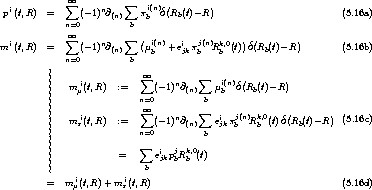

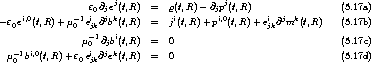



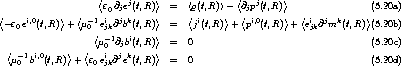


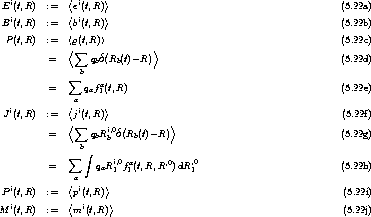

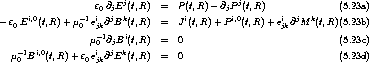




 d.h. bei
d.h. bei  ) und auf den
Oberfläche
) und auf den
Oberfläche d.h. bei
d.h. bei  ) die tatsächlichen Flächen-Ladungsdichte
) die tatsächlichen Flächen-Ladungsdichte






 und +
und + :
: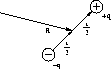
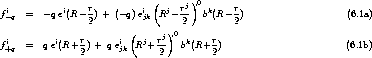

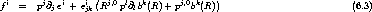
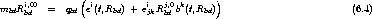




 ) erzeugten Felder
) erzeugten Felder



 ) Elektronen des eigenen Atoms erzeugten Felder
) Elektronen des eigenen Atoms erzeugten Felder
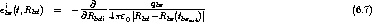





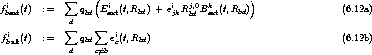



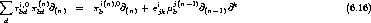

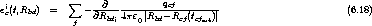
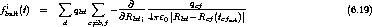
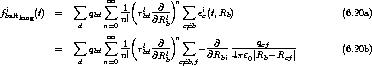
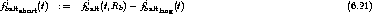


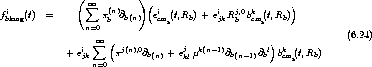
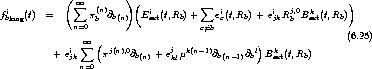

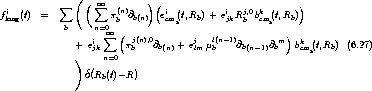

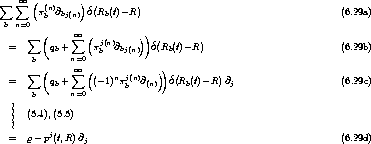
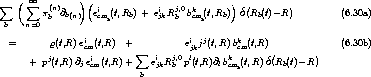
 also den Atom-
Indicem “
also den Atom-
Indicem “ ”
” ). Zielvorstellung der weiteren Umformungen wird die Interpretation der
“störenden” Atom-Geschwindigkeit
). Zielvorstellung der weiteren Umformungen wird die Interpretation der
“störenden” Atom-Geschwindigkeit  im Rahmen einer totalen zeitlichen Ableitung
sein. Mit dieser Perspektive schlüsseln wir den ganzen Term mit der Vektor-Identität
im Rahmen einer totalen zeitlichen Ableitung
sein. Mit dieser Perspektive schlüsseln wir den ganzen Term mit der Vektor-Identität
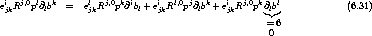


 ” sich nicht mit der Zeit ändert. Bei zeitabhängigem
Magnetfeld ist sehr wohl darauf zu achten, wie der Kelvin-Term verjüngt wird. Hier hätte eine
ausreichend explizite Schreibweise dem Leser wissenschaftlicher Literatur sicher manch’ irrige
Interpretationem erspart7.
” sich nicht mit der Zeit ändert. Bei zeitabhängigem
Magnetfeld ist sehr wohl darauf zu achten, wie der Kelvin-Term verjüngt wird. Hier hätte eine
ausreichend explizite Schreibweise dem Leser wissenschaftlicher Literatur sicher manch’ irrige
Interpretationem erspart7.
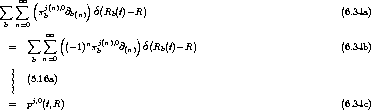


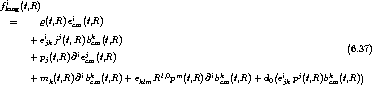



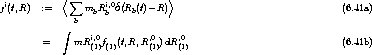

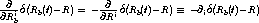
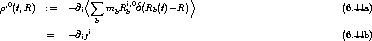




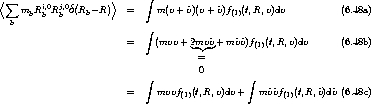




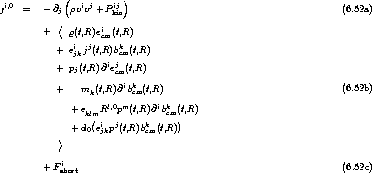
 siehe (
siehe ( ) kann man die
Ensemble-Mittelung
) kann man die
Ensemble-Mittelung
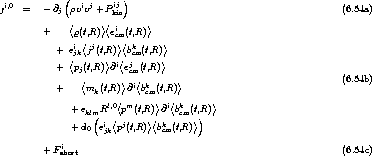

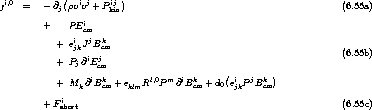






 ) über via [thermodynami
) über via [thermodynami
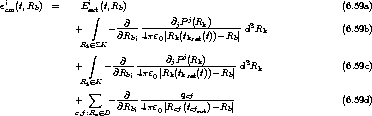
 beschreibende Term (
beschreibende Term (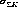 entspricht:
entspricht:










 ,
,



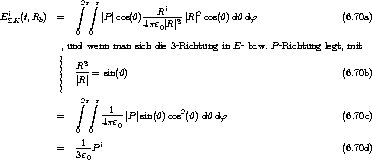



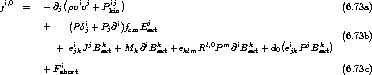

 i.e. Rand
i.e. Rand ) von
) von 
![integral
dU = 1 e (deE E + edE E + eEdE) dv (7.3a)
2 0
[Vtot integral integral ]
+ 1 e deE E dv- 1 e deEE dv (7.3b)
2 0 2 0
integral integral
= EdD dv+ 1 e0deE E dv (7.3c)
Vtot 2Vtot](arbeit244x.gif)


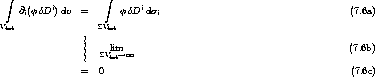






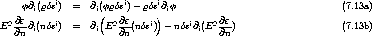




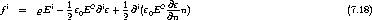









![ij ~ k
s Oidhj = d(F O hk) (7.25a)
= [d~F (dO)khk + ]F~Ok(dh)k + d~F Okhk (7.25b)](arbeit269x.gif)




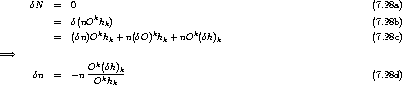
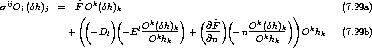








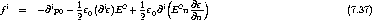
 im SO(3)-Falle ist z.B.
im SO(3)-Falle ist z.B.  )
) 



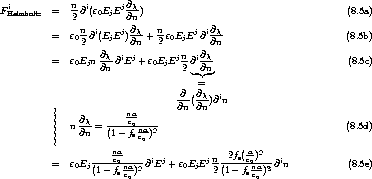

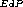 ist die in der Aufspreizung der
Dipole gespeicherte potentielle Energie, was man sich am Modell des aufgeladen werdenden
Kondensatoris klarmachen kann.
ist die in der Aufspreizung der
Dipole gespeicherte potentielle Energie, was man sich am Modell des aufgeladen werdenden
Kondensatoris klarmachen kann.
 außerdem wurde noch die Variable
außerdem wurde noch die Variable  ):
): 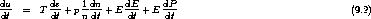






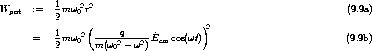

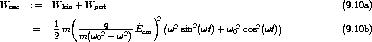

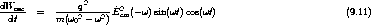



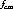 nur in einfacher Potenz auftritt.
nur in einfacher Potenz auftritt.








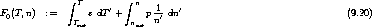

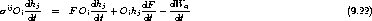

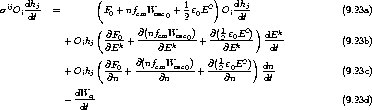
 zu gewährleisten. Diese Leistung haben wir zwar
mechanisch erbracht, sie kam jedoch nicht unserem Dielektriko zugute, sondern eben dem
Ladungsbad.
zu gewährleisten. Diese Leistung haben wir zwar
mechanisch erbracht, sie kam jedoch nicht unserem Dielektriko zugute, sondern eben dem
Ladungsbad.
 auszuklammern.
auszuklammern.

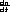 gemäß (
gemäß (




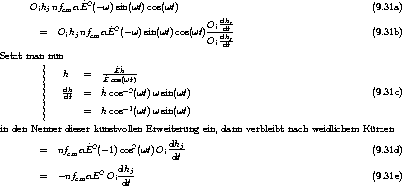



 ausfaktoriert wurde, können wir die Co-Faktores zum
Spannungstensor
ausfaktoriert wurde, können wir die Co-Faktores zum
Spannungstensor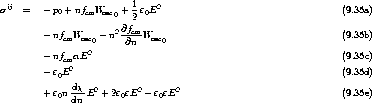

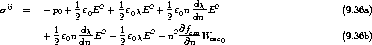


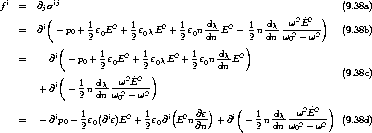
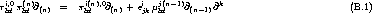
 , der Definitioni für elektrische Monopol
, der Definitioni für elektrische Monopol (
( (
( ), der Ladungserhaltung
), der Ladungserhaltung , der nullten Ableitung
, der nullten Ableitung
 und der Nicht-Existenz magnetischer Monopol
und der Nicht-Existenz magnetischer Monopol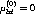 (
( (
( ),
),

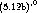 .
.




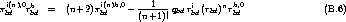
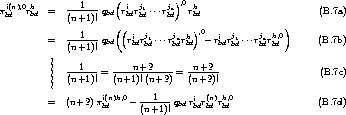
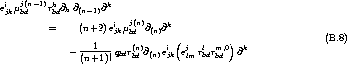
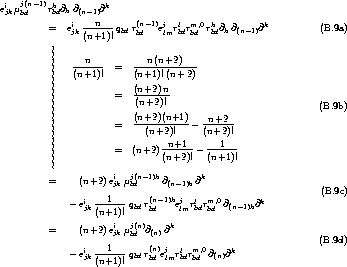
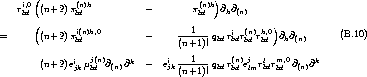
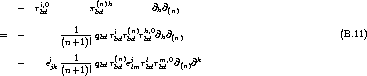

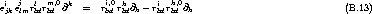
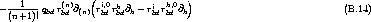
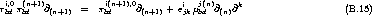
 in dem Sinne, daß man nur einen Parameter
in dem Sinne, daß man nur einen Parameter  ) durch die Transformationsgruppe
) durch die Transformationsgruppe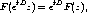
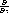 und
und  . Panofsky und Melba Phillips.
. Panofsky und Melba Phillips.